Consider two sources A and B as shown in the figure below. Let the two sources emit simple harmonic waves of same frequency but of different amplitudes, and both are in phase (same phase). Let O be any point equidistant from A and B as shown in the figure. Calculate the intensity at points O, Y and X. (X and Y are not equidistant from A & B)

The distance between OA and OB are the same and hence, the waves starting from A and B reach O after covering equal distances (equal path lengths). Thus, the path difference between two waves at O is zero.
OA - OB = 0
Since the waves are in the same phase, at the point O, the phase difference between two waves is also zero. Thus, the resultant intensity at the point O is maximum.
Consider a point Y, such that the path difference between two waves is λ. Then the phase difference at Y is
Δφ=2πλ×Δr=2πλ×λ=2π
Therefore, at the point Y, the two waves from A and B are in phase, hence, the intensity will be maximum.
Consider a point X, and let the path difference the between two waves be λ2. Then the phase difference at X is
Δφ=2πλλ2=π
Therefore, at the point X, the waves meet and are in out of phase, Hence, due to destructive interference, the intensity will be minimum.
Topper's Solved these Questions
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(I. MULTIPLE CHOICE QUESTIONS)
15 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
- UNITS AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE (ADDITIONAL EXERCISE)
9 Videos
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE - IV. NUMERICAL PROBLEMS
5 Videos
Similar Questions
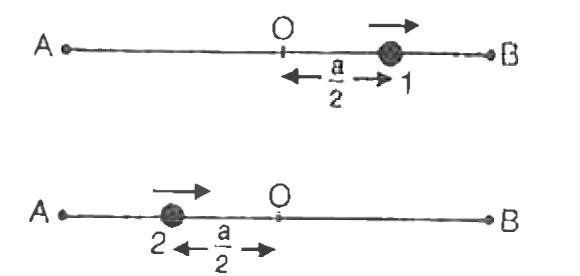
Two bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png)
View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
View Solution
Knowledge Check
Two bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png) A116πBπC53πD35π
A116πBπC53πD35πWhen two waves of the same frequency and same amplitude ‘a’ are superposed in phase, the resulting intensity at the point of superposition is proportional to
A4a2B2a2C2aD0If a point (x,y) is equidistant from the points A(9,8) and B(17,8), then the relation between x and y is :
Ax+y=13Bx−13=0Cy−13=0Dx−y=13
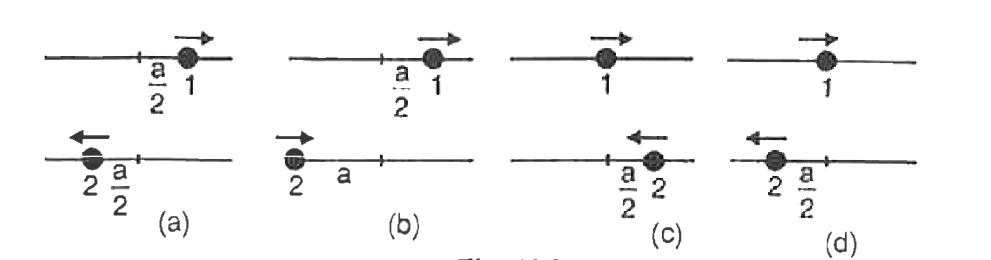
Find the phase difference between two particles executing simple harmonic motion with the same frequency if they are found inn the states shown in the figures at four different points of time.
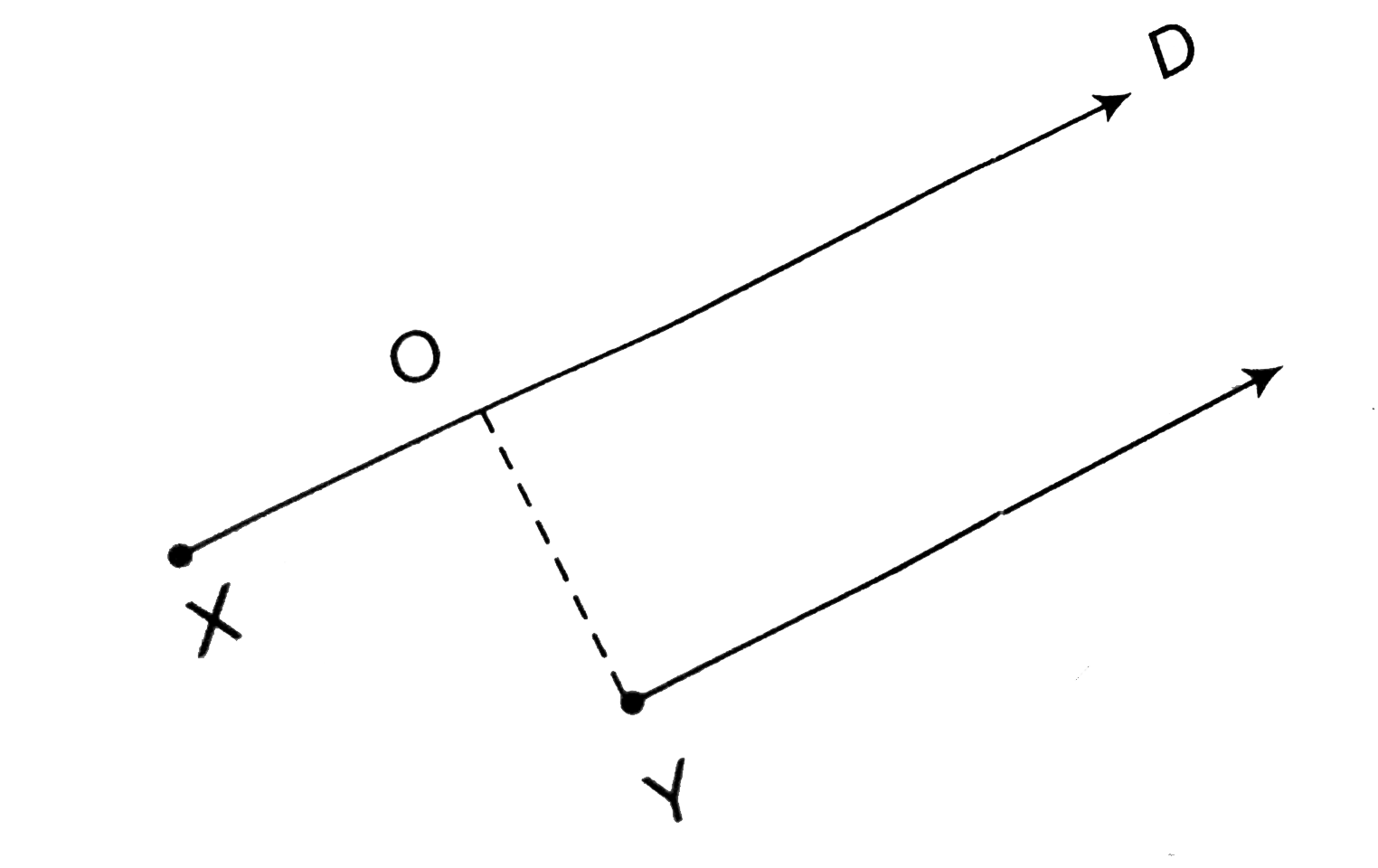
View SolutionTwo point sources X and Y emit waves of same frequency and speed but Y lags in phase behind X by 2π/radian. If there is a maximum in direction D the distance XO using n as an integer is given by

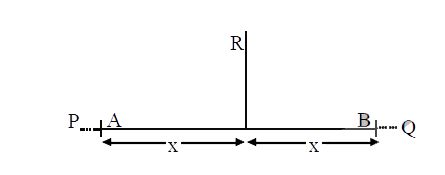
View SolutionThe frequencies of sources A and B as shown in figure are same. The nature of interference at points P, Q and R will be if AB=λ2 and the two sources are in same phase.
View SolutionTwo point sources X and Y emit waves of same frequency and speed but Y lags in phase behind X by 2π/radian. If there is a maximum in direction D the distance XO using n as an integer is given by

View SolutionTwo point sources X and Y emit waves of same frequency and speed but Y lags in phase behind X by 2πd radian. If there is a maximum in direction D, the distance XO using n as an integer is given by
View Solution
