Question

Two speakers C and E are placed 5 m apart and are driven by the same source. Let a man stand at A which is 10 m away from the mid point O of C and E. The man walks towards the point O which is at 1 m (parallel to OC) as shown in the figure. He receives the first minimum in sound intensity at B. Then calculate the frequency of the source. (Assume speed of sound = 343 m $s^{-1}$)

Explanation

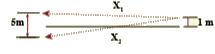
The first minimum occurs when the two waves reaching the point B are `180^@` (out of phase). The path difference `Delta x = lambda/2`.
In order to calculate the path difference, we have to find the path lengths `x_1` and `x_2`.
In a right triangle BDC,
DB = 10m and `OC=1/2(5)=2.5m`
`CD = OC-1=(2.5 m)-1m=1.5 m`
`x_1=sqrt((10)^2+(1.5)^2)=sqrt(100+2.25)`
`=sqrt(102.25) = 10.1 m`
In a right triangle EFB,
DB = 10m and `OE = 1/2 (5) = 2.5m = FA`
FB = FA + AB = (2.5 m) + 1 m = 3.5 m
`x_2=sqrt((10)^2+(3.5)^2)=sqrt(100+12.25)=sqrt(112.25)` = 10.6m
The path difference `Delta x = x_2-x_1` = 10.6 m - 10.1m = 0.5m. Required that this path difference
`Delta x=lambda/2 =0.5 implies lambda=1.0 m`
To obtain the frequency of source, we use
`v=lambda f implies f=v/lambda=(343)/(1)=343 Hz`
= 0.3 kHz