A fish looking up through the water sees the outside world contained in circular horizon. If the R.I. of water 43 and tne fish is 12 cm below the surface, the radius of this circle in cm is-
36√7
36√7
36√5
4√5
The correct Answer is:B
To solve the problem, we need to find the radius of the circular horizon that a fish sees when looking up through the water. We will use the formula for the radius of the circular region visible to the fish, which is derived from the refractive index of the medium.
1. Identify the Given Values:
- Refractive Index (R.I.) of water, n=43
- Depth of the fish below the surface, h=12cm
2. Use the Formula for the Radius:
The formula for the radius R of the circular horizon is given by:
R=h√n2−1
3. Substitute the Values into the Formula:
First, we need to calculate n2−1:
n2=(43)2=169
Therefore,
n2−1=169−1=169−99=79
4. Calculate the Square Root:
Now, we take the square root of n2−1:
√n2−1=√79=√73
5. Substitute Back into the Radius Formula:
Now we substitute back into the radius formula:
R=12√79=12√73=12×3√7=36√7
6. Final Result:
The radius of the circular horizon that the fish sees is:
R=36√7cm
- Refractive Index (R.I.) of water, n=43
- Depth of the fish below the surface, h=12cm
The formula for the radius R of the circular horizon is given by:
R=h√n2−1
First, we need to calculate n2−1:
n2=(43)2=169
Therefore,
n2−1=169−1=169−99=79
Now, we take the square root of n2−1:
√n2−1=√79=√73
Now we substitute back into the radius formula:
R=12√79=12√73=12×3√7=36√7
The radius of the circular horizon that the fish sees is:
R=36√7cm
Topper's Solved these Questions
Similar Questions
A fish in a water tank sees the outside world as if it (the fish) is at the vertex of cone such that the circular base of the cone coincides with the surface of water. Given the depth of water where fish is located being h and the critical angle for water - air interface being iC, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height h.
View SolutionA fish in a water tank sees the outside world as if it (the fish) is at the vertex of cone such that the circular base of the cone coincides with the surface of water. Given the depth of water where fish is located being h and the critical angle for water-air interface being ic, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height h.
View Solution
Knowledge Check
A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 4/3 and the fish is 12cm below the surface, the radius of this circle in cm is
A36√5B4√5C36√7D36/√7A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle is cm is
A36√7B36√7C4√5D36√5A fish looking up through the wave sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle in cm is
A36√5B4√5C36√7D36sqry7
A diver looking up through the water sees the outside world contained in a circular horizon. The refractive index of water is 43, and the diver's eyes are 15 cm below the surface of 3 water. Then the radius of the circle is:
View SolutionA fist looking from within water sees the outside world through a circular horizon. If the fish √7 cm below the surface of water, what will be the radius of the circular horizon
View SolutionA fish at a depth of √7 cm bleow the surface of water sees the outside world through a circular horizon. What is the radius of the circular horizon? [aμw=43]
View SolutionA man looks down on a fish of length 20 cm. His eye is 2m above the surface of the water (μ=4/3) and the fish is 2m below the surface as shown in the figure the ratio of angular width Δθ of the fish as seen by the man in presence of water to the Δθ in the absence of water is (Δθ is small)
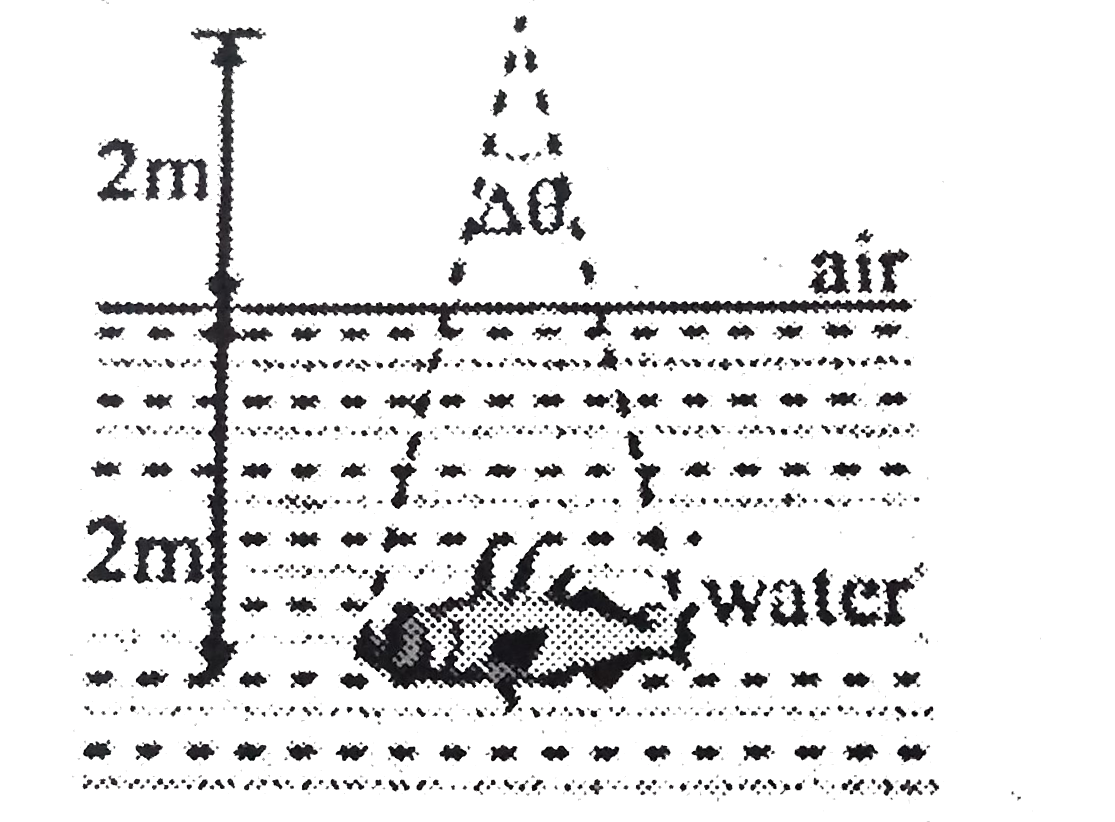
View SolutionA fish situated at a depth h below the surface of water in a lake ,can see the outside objects in air through a circular aperature of radius r . What is the radius of the aperture in terms of h and n ,where n=anw? [anw = R.I. of water w.r.t. air]
View Solution
