In the given set up the light of wavelength 5000A is used incident normally on the slits. The screen is at a distance D = 80 cm from a diaphragm having two narrow slits S1 and S2 which are d = 2 mm apart. Slit S1 is covered by a transparent sheet of thickness t2=1.25μm and slit S2 is covered by another sheet of the same material of the thickness t2=1.25μm. (as in the figure). Water is filled in the space between diaphragm and screen. Assuming intensity of beam to be uniform, calculate the ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (μw=43,μsheet=1.40)

The correct Answer is:00.75
Path difference at C
Δx=t1(μ−1)−t2(μ−1)
=(t1−t2)(μsμw−1)
=(2.5−1.25)(14×34×10−1)μm
=25400μm
=116μm
⇒ϕ=2πλ×Δx
=2π×45000×10−10×3×116×10−6(x2−x4)
=π3
⇒Imax=4I0
Intensity at C,IC=2I0(1+cosπ3)=3I0
Required ratio =1L1=34=0.75
Topper's Solved these Questions
Similar Questions
Find the decay constant (per minute) of a radioactive sample if at any instant its disintegration rate is 5000 disintegrations per minute and after 5 minutes, the rate is 1250 disintegrations per minute.
View SolutionIn the given reaction
ZXA→ZYA+nα+n'β.The ratio (Z'A') will be equal to
View SolutionA screen is at distance D = 80 cm form a diaphragm having two narrow slits S_(1) and S_(2) which are d = 2 mm apart. Slit S_(1) is covered by a transparent sheet of thickness t_(1) = 2.5 mu m slit S_(2) is covered by another sheet of thikness t_(2) = 1.25 mu m as shown if Fig. 2.52. Both sheets are made of same material having refractive index mu = 1.40 Water is filled in the space between diaphragm and screen. Amondichromatic light beam of wavelength lambda = 5000 Å is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (mu_(w) = 4//3)
View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
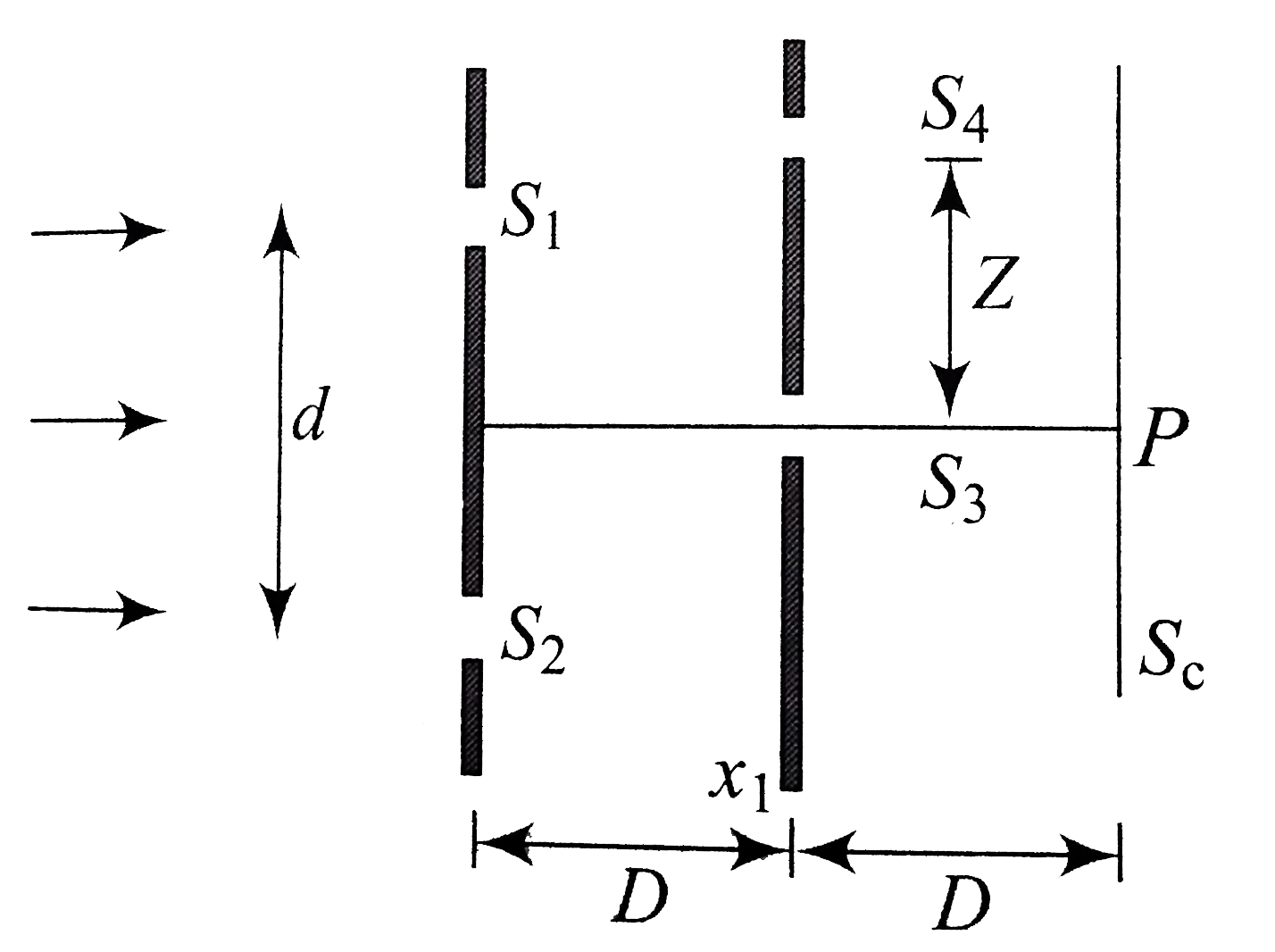
If z=λDd
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
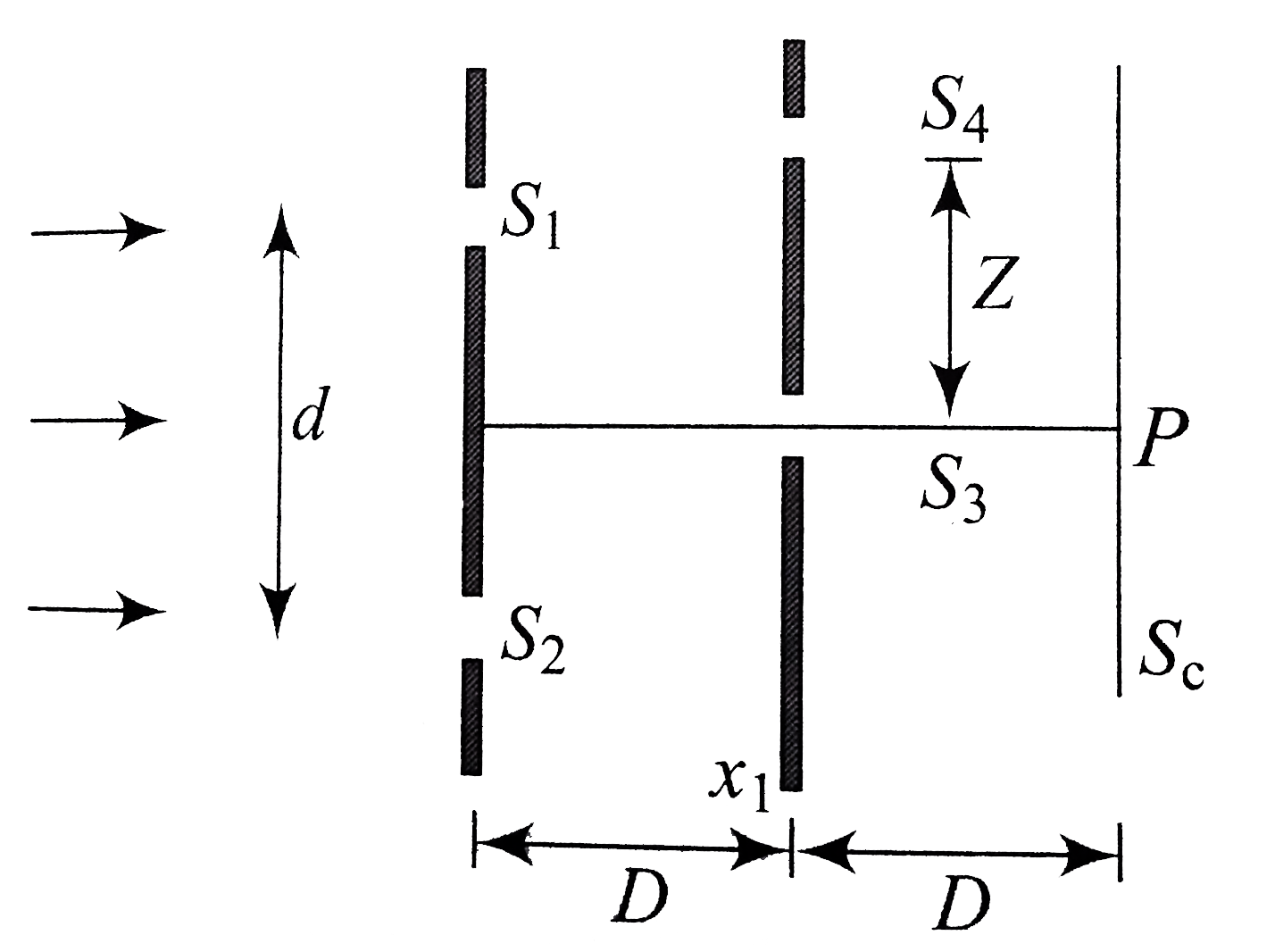
If z=λD4d
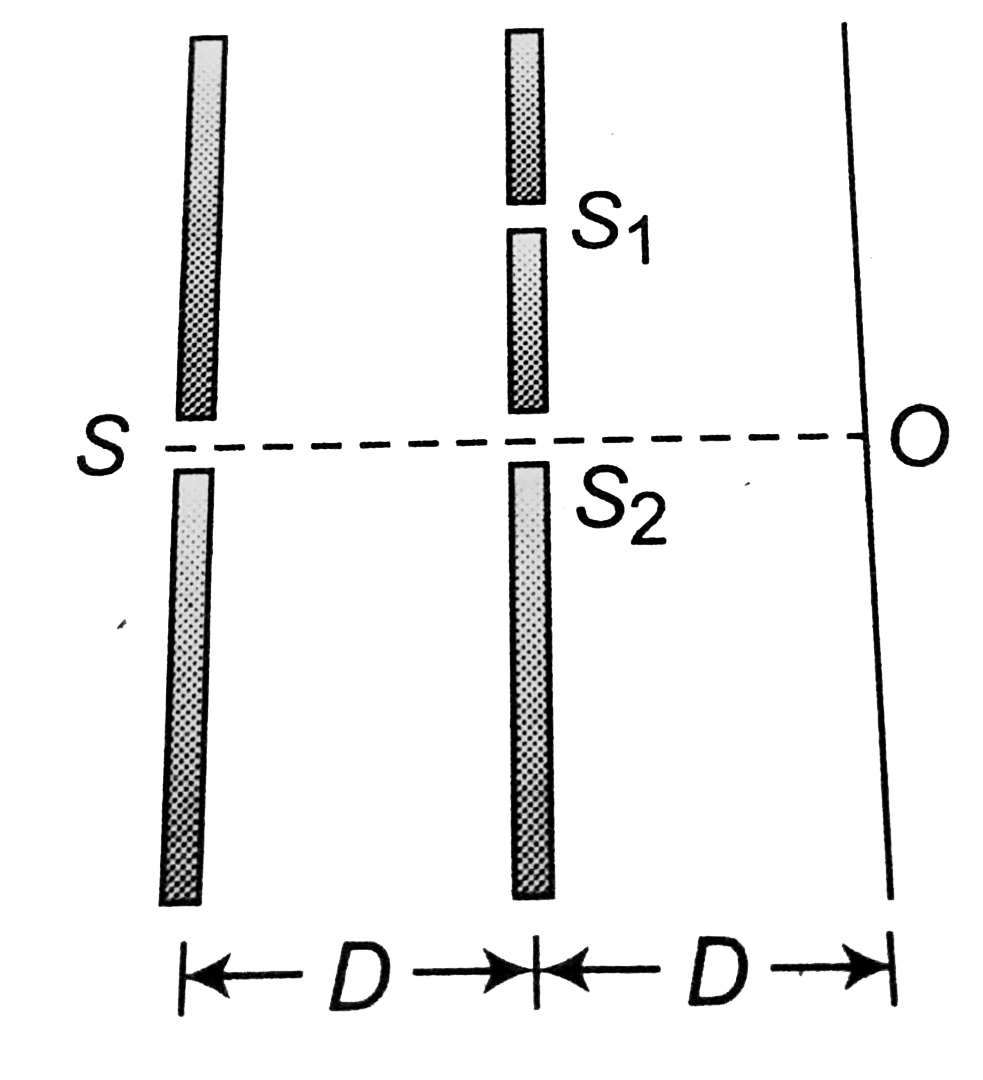
View SolutionTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d

View SolutionA plane monochromatic light falls normally on a diaphragm with two narrow slits separated by a distance d = 2.5 mm. A fringe pattern is formed on the screen placed at D = 100 cm behind the diaphragm. If one of the slits is covered by a glass plate of thickness 10mu m , then distance by which these fringes will be shifted will be :
View SolutionIn Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is
View SolutionMonichromatic lightof wavelenght 600 nm is used ina Young's double slilt experient. One of the slits is covered by a transparent sheet of thicknes 1.8×10−5 m made of a material of refractive index 1.6. How many fringe will shift due to the introduction of the sheet?
View SolutionLight of wavelength lambda = 500 nm falls on two narrow slits placed a distance d = 50 xx 10^(-4) cm apart, at an angle phi = 30^(@) relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mmand refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits S_(1)O = S_(2)O = d//2 The interference minima closest to B is of order
View SolutionIn a Young's double slit experiment, a monochromatic source of wavelength λ is used to illuminate the two slits S1 and S2.

The slits S1 and S2 are identical and source S is placed symmetrical as shown. Interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the size of slit S1 is slightly decreased, then
View SolutionConsider the situation shown in figure , The two slits S1andS2 placed symmetrically around the central line are illumated by a monocharmotic by a monocharomatic light of wavelength λ . The separation between the slits is d . The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits . The slit S3 is at the central line and the slit S4 is at a distance z from S3 .Another screen Σ2 is placed a further distance D away from Σ1 .Find the ratio of the minimum intensity observed on Σ2 if z is equal to
(1) z=λD2d
(2) λDd
(3) λD4d
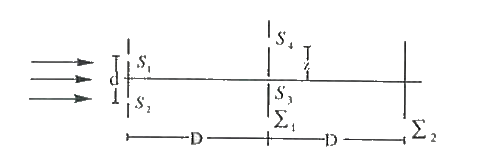
View SolutionLight of wavelength λ=500 nm falls on two narrow slits placed a distance d=50×10−4 cm apart, at an angle ϕ=30∘ relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mm and refractie index 3/2 is placed. THe interference pattern is observed on a screen at a distance D= 2m from the slits S1O=S2O=d/2

If the transparent slab is removed the fringe pattern shifts upward , the number of frings shifted upward are
View SolutionIn a Young.s double slit experiment , a monochromatic source if wavelength lambda is used to illmunate the two slits S_(1) and S_(2) The slits S_(1)and S_(2) are identical and source S is placed symmetrically as shown .Interference pattern is observed on a screen at a distance D from the centre of slit . The distance between the slits is d .If the size of slit S_(1) is slightly decreased , them
View Solution
