A rod AB of mass m and length l is rotating about a vertical axis as s

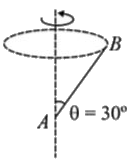
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle $θ$ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed $V$ in the horizontal plane then the angular momentum of the rod about the axis is:
A $\frac{1}{2} m V L cos θ$
B $\frac{1}{3} m V L sin θ$
C $m V L sin cos θ$
Dzero
A wire of mass $m$ and length $l$ is bent in the form of circular ring. The moment of inertia of the ring about its axis is
A $m l^{2}$
B $\frac{m l^{2}}{4 π^{2}}$
C $\frac{m l^{2}}{2 π^{2}}$
D $\frac{m l^{2}}{8 π^{2}}$
A thin rod of mass $M$ and length $L$ is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
A $\frac{M L^{2}}{2 π^{2}}$
B $\frac{M L^{2}}{4 π^{2}}$
C $\frac{M L^{2}}{8 π^{2}}$
D $\frac{M L^{2}}{π^{2}}$

A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :