A monoatomic gas expands following as thermodynamic law P=C1V+C2, where C1,C2 are constants, from state A(V0,3P0) to B(3V0,P0).What will be the volume of the gas upto which it absorbs heat?
V0
2V0
2.5V0
3V0
The correct Answer is:C
The gas absorbs heat till
dPdV=−γPV
−P0V0=−53PV
⇒P=3P05V0V
Putting in the equation
3P05V0V=−P0V0+4P0
⇒V=2.5V0
Topper's Solved these Questions
Similar Questions
Knowledge Check
For one mole of ideal gas if P=P01+(VV0) where P0 and V0 are constant, then temperature of gas when V=V0 is:
AP0V0RBP0V04RCP0V02RDP0V03RFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
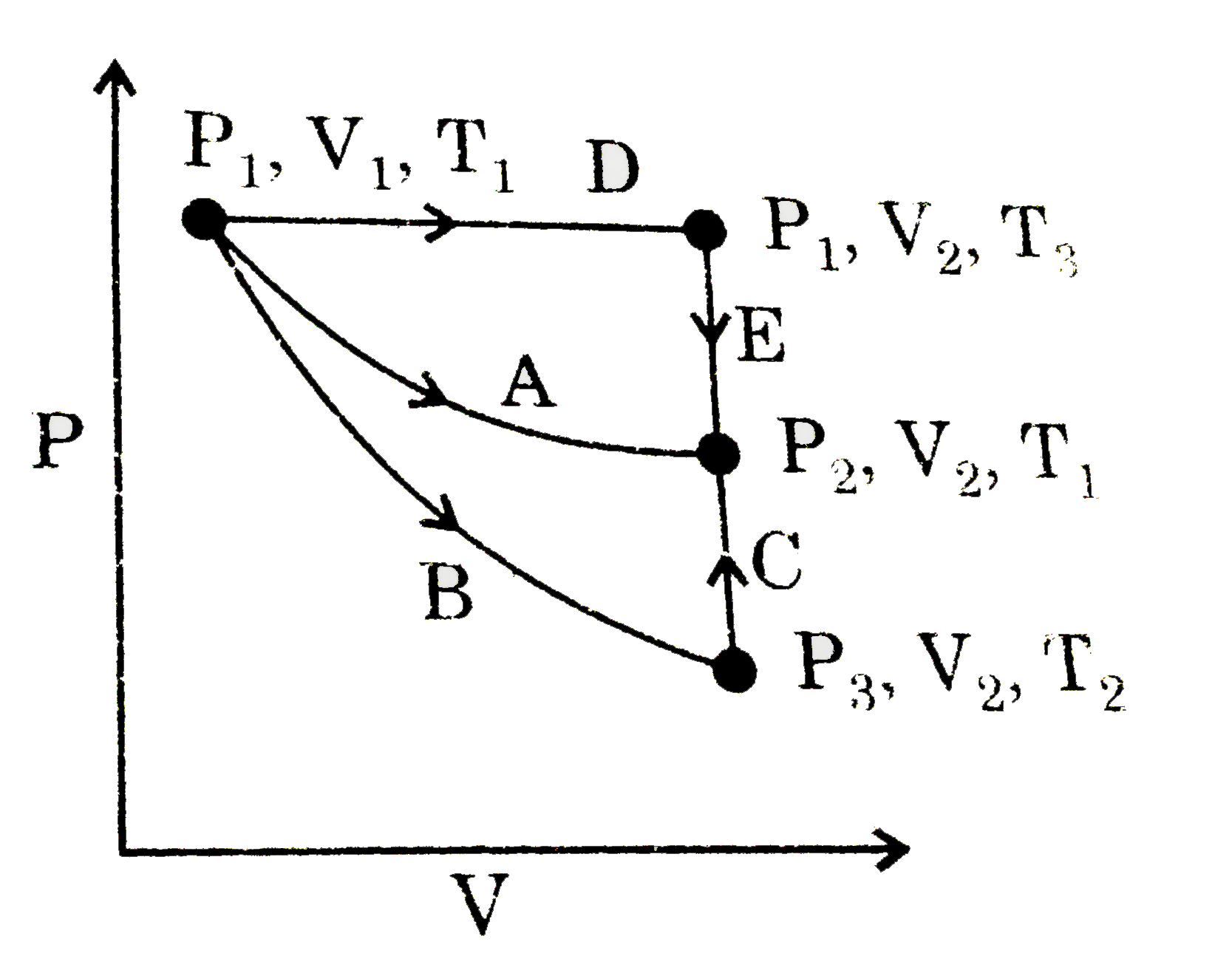
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?AzeroB−nR InV2V1C−nRT1 InV2V1DnRT1 InV2V1For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?AzeroB∫T1T3CV(T)TdtC−nR InV2V1DnR InV2V1
One mole of an ideal gas undergoes a process
p=p01+(VV0)2
where p0and V0 are constants. Find temperature of the gaas when V=V0.
View SolutionOne mole of a diatomic gas undergoes 'a process P=P01+(VV0)s, where P0,V0 are constants. The translational kinetic energy of the gas when V=V0 is given by αP0V0β, Find (α+β).
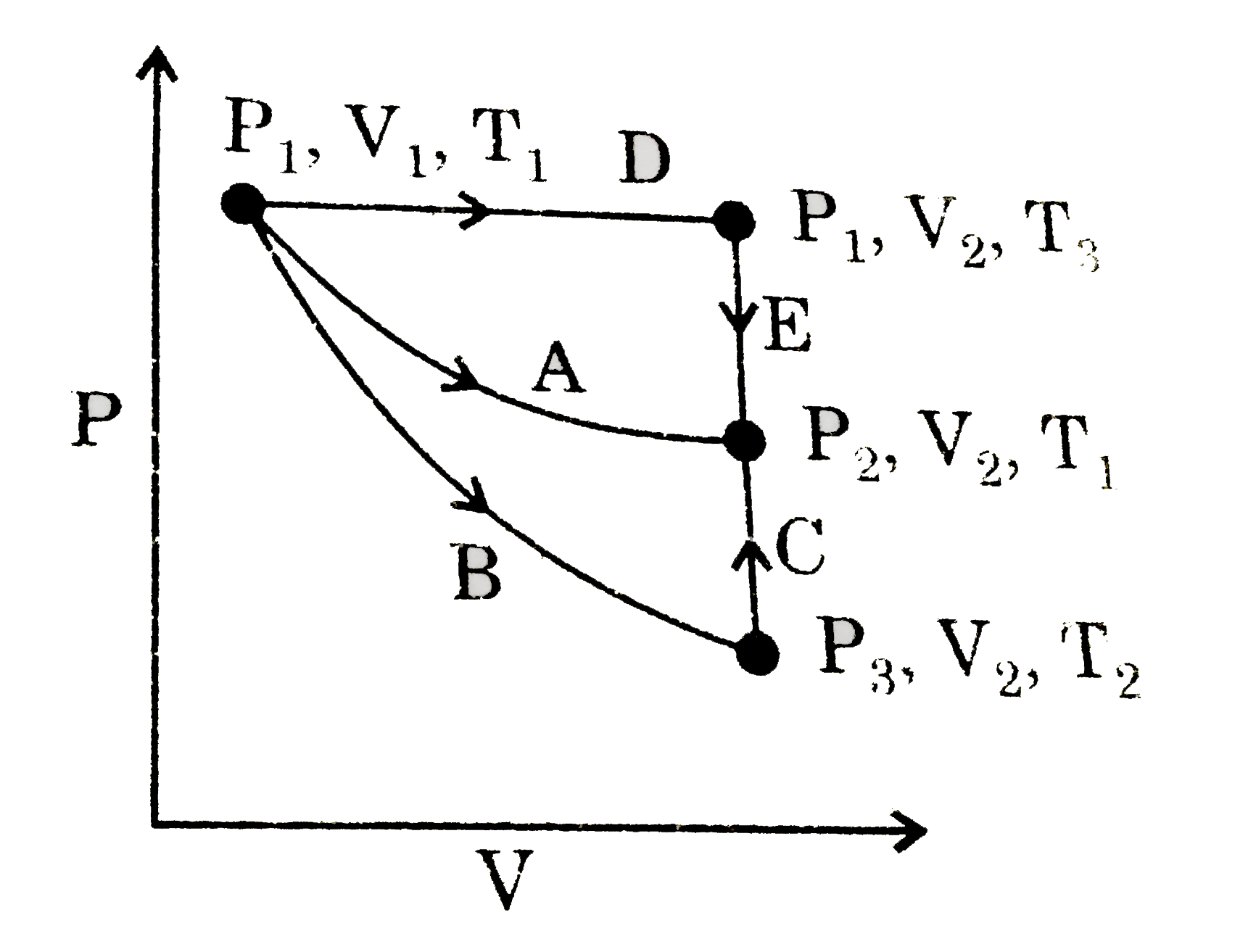
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .

Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (B+C)?
View SolutionCpCV for Monoatomic gas molecule is
View Solution
