A uniform cylinder of radius R(=3m) is spun about its axis at an angular velocity
ω0(=40√kπradsec−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=0.2). If this cylinder makes N turns before it stops then findthe value of N100
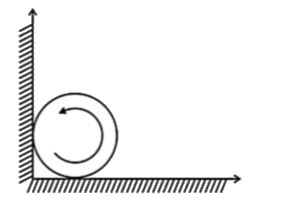
The correct Answer is:2.60
N1=μN2
N2+μN1=mg
μ(N1+N2)R=(mR22)α
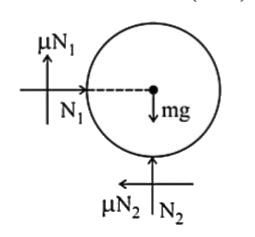
0=ω20−2αθ
N=θ2π
Topper's Solved these Questions
Similar Questions
A uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity ω0(=40√π rad s−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=2). Then, how many rotations will the cylinder make before it comes to rest?
View SolutionA uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

View Solution
Knowledge Check
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgA uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then
 Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of these
Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of theseA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
A0.2 J sB1.12 J sC0.12 J sD12 J s
A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?

View SolutionA uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
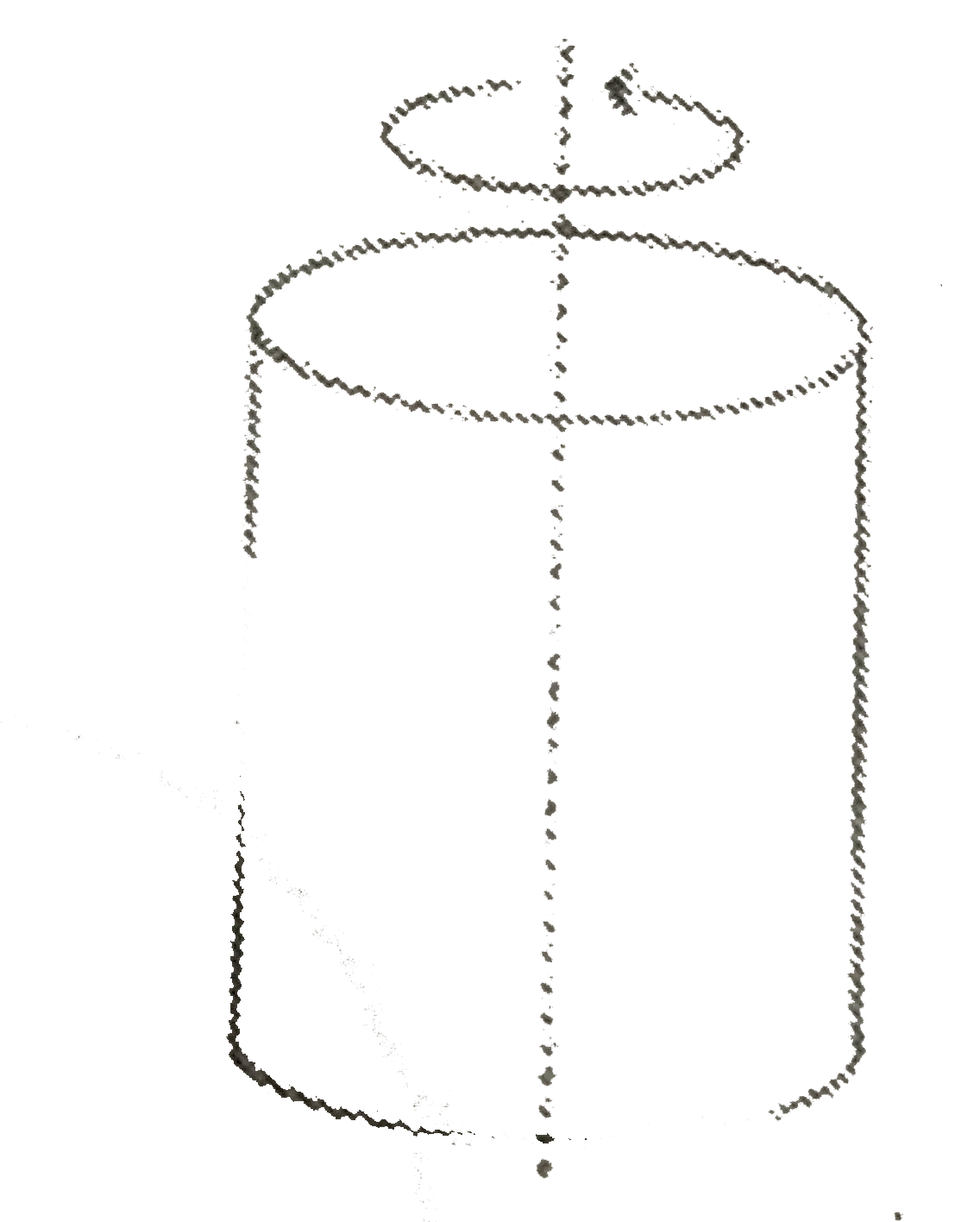
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?

View Solution
