As in the figure if a spherical cavity (centered at O) of radius 1 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e. on the surface of the cavity R can be determined by the equation:
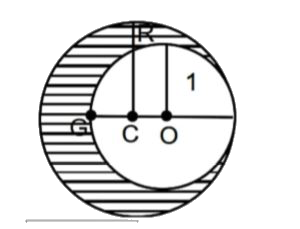
(R2−R+1)(2−R)=1
(R2+R+1)(2−R)=1
(R2−R−1)(2−R)=1
(R2+R−1)(2−R)=1
The correct Answer is:B
M1=43πR3ρ
M2=43π(1)(3)(−ρ)
M2=43π(1)3(−ρ)
Xcom=M1X1+M2X2M1+M2
⇒[43πR3ρ]0+[43π(1)3(−ρ)][R−1]43πR3ρ+43(1)3(−ρ)=
−(2−R)
⇒(R−1)(R3−1)=(2−R)
⇒(R−1)(R3−1)=(2−R)(R≠1)
(R−1)(R−1)(R2+R+1)=2−R
(R2+R+1)(2−R)=1
Alternative:
Mremaining (2−R)=M cavity(1−R)
⇒(R3−13)(2−R)=13[R−1]
⇒(R2+R+1)(2−R)=1
Topper's Solved these Questions
Similar Questions
As shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
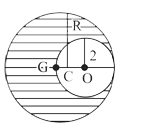
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:

View Solution
Knowledge Check
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1
A(R2+R+1)(2–R)=1B(R2–R–1)(2–R)=1C(R2–R+1)(2–R)=1D(R2+R–1)(2–R)=1A uniform metal disc of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
AR4 from the centerBR3 from the centerCR5 from the centerDR6 from the center.
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View SolutionA uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
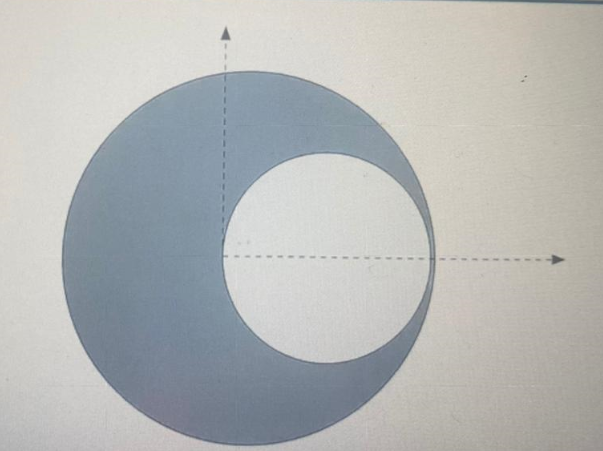
View SolutionIf a solid cavity whose diameteris removed from a solid sphere of radius R then the com of remaining part is at
View Solution
