In Fig. 4.192, ABC is a right triangle right-angled at B . AD and CE are the two medians drawn from A and C respectively. If AC=5cm and AD=3√52cm , find the length of CE . (FIGURE)
To solve the problem step by step, we will use the properties of right triangles and medians.
Step 1: Understand the triangle and medians
Given triangle ABC is a right triangle with the right angle at B. The lengths provided are:
- AC=5cm
- AD=3√52cm (median from A to D)
Step 2: Use the median formula in triangle ADB
In triangle ADB, we can use the median length formula. Since D is the midpoint of BC, we know:
AD2=AB2+(BC2)2
Let AB=x and BC=y. Thus, we can rewrite the equation as:
AD2=x2+(y2)2
Substituting AD=3√52:
(3√52)2=x2+(y2)2
Calculating AD2:
454=x2+y24
Multiplying through by 4 to eliminate the fraction:
45=4x2+y2(Equation 1)
Step 3: Use the median formula in triangle EBC
In triangle EBC, where E is the midpoint of AC:
CE2=BC2+(AB2)2
Substituting CE and using AB=x and BC=y:
CE2=y2+(x2)2
Thus:
CE2=y2+x24(Equation 2)
Step 4: Relate the two equations
Since triangle ABC is a right triangle, we can apply the Pythagorean theorem:
AC2=AB2+BC2
Substituting AC=5:
25=x2+y2(Equation 3)
Step 5: Substitute Equation 3 into Equation 1
From Equation 3, we have y2=25−x2. Substitute this into Equation 1:
45=4x2+(25−x2)
Simplifying:
45=4x2+25−x2
45−25=3x2
20=3x2
x2=203
Step 6: Substitute x2 back to find y2
Using Equation 3:
y2=25−x2=25−203=753−203=553
Step 7: Substitute x2 and y2 into Equation 2
Now substitute x2 and y2 into Equation 2 to find CE2:
CE2=y2+x24=553+20/34=553+53=603=20
Step 8: Find CE
Taking the square root:
CE=√20=2√5cm
Final Answer:
The length of CE is 2√5cm.
---
Given triangle ABC is a right triangle with the right angle at B. The lengths provided are:
- AC=5cm
- AD=3√52cm (median from A to D)
In triangle ADB, we can use the median length formula. Since D is the midpoint of BC, we know:
AD2=AB2+(BC2)2
Let AB=x and BC=y. Thus, we can rewrite the equation as:
AD2=x2+(y2)2
Substituting AD=3√52:
(3√52)2=x2+(y2)2
Calculating AD2:
454=x2+y24
Multiplying through by 4 to eliminate the fraction:
45=4x2+y2(Equation 1)
In triangle EBC, where E is the midpoint of AC:
CE2=BC2+(AB2)2
Substituting CE and using AB=x and BC=y:
CE2=y2+(x2)2
Thus:
CE2=y2+x24(Equation 2)
Since triangle ABC is a right triangle, we can apply the Pythagorean theorem:
AC2=AB2+BC2
Substituting AC=5:
25=x2+y2(Equation 3)
From Equation 3, we have y2=25−x2. Substitute this into Equation 1:
45=4x2+(25−x2)
Simplifying:
45=4x2+25−x2
45−25=3x2
20=3x2
x2=203
Using Equation 3:
y2=25−x2=25−203=753−203=553
Now substitute x2 and y2 into Equation 2 to find CE2:
CE2=y2+x24=553+20/34=553+53=603=20
Taking the square root:
CE=√20=2√5cm
The length of CE is 2√5cm.
Topper's Solved these Questions
Similar Questions
In Fig. 4.192, ABC is a right triangle right-angled at B . AD and CE are the two medians drawn from A and C respectively. If AC=5cm and AD=3√52cm , find the length of CE . (FIGURE)
View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
View Solution
Knowledge Check
In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
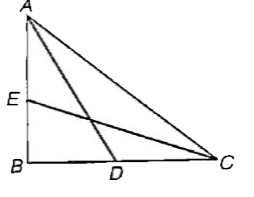 A2√5cmB2.5cmC5cmD4√2cm
A2√5cmB2.5cmC5cmD4√2cmIn figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
 A2 cmB2√5 cmC5√2 cmD3√2 cm
A2 cmB2√5 cmC5√2 cmD3√2 cmIn a right triangle with legs a and b and hypotenuse c, angles A,B and C are opposite to the sides a,b and c respectively, then elnb−lna is equal to-
AsinABcotBCtanADcotA
In Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
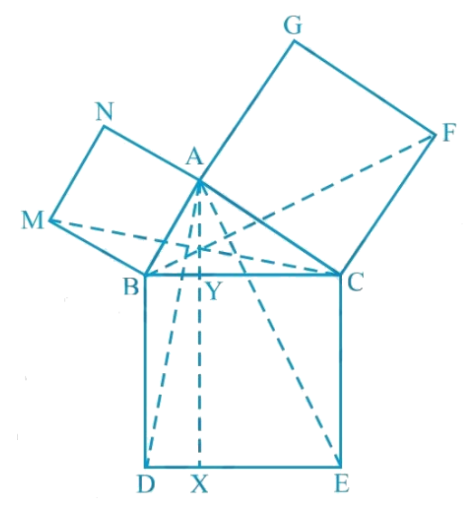
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
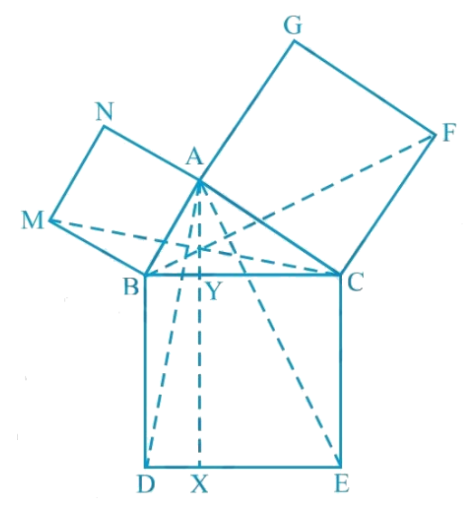
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
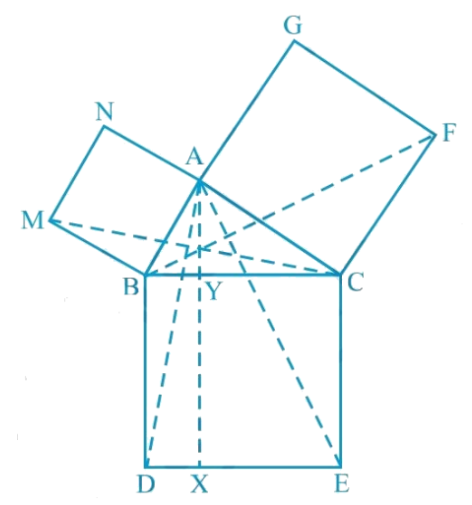
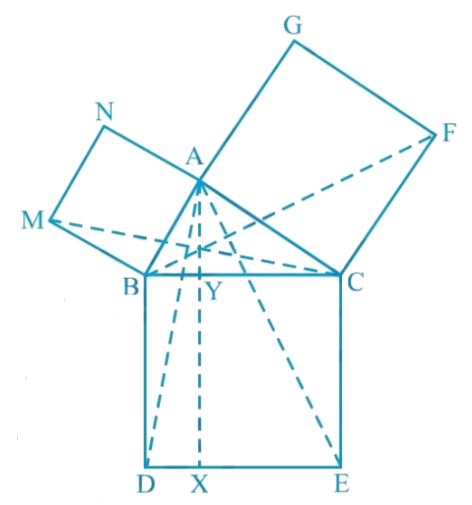
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
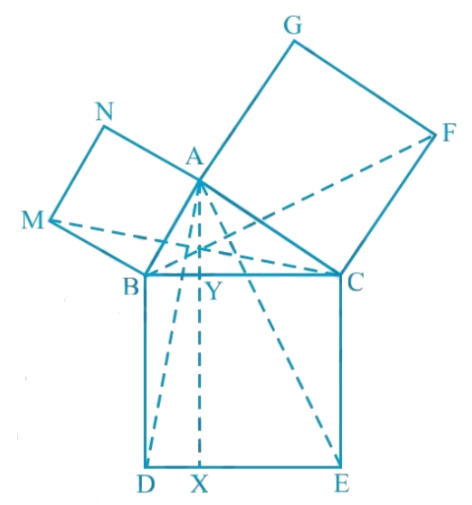
View Solution
