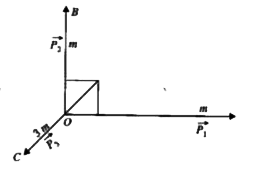
A body of mass 1 kg is initially at rest. It explodes into three pieces of masses in the ratio $1 : 1 : 3$ . Two pieces of equal masses fly off perpendicular to each other with a speed of $30 m / s$ . What is the velocity of the heavier mass ?

Text Solution

Verified by Experts

Let the mass of the three fragments be m kg, m kg, and 3m kg.
Total mass = 1kg
So $m + m + 3 m = 1 k g$
$5 m = 1 k g, m = \frac{1}{5} k g$
Momentum along OA is $P_{1} =$ Mass $\times$ Velocity
$= \frac{1}{5} \times 30 = 6 k g m s^{- 1}$
$P_{2} = 6 k g m s^{- 1}$
$P_{3} = 3 m \times v$
v velocity of the 3rd piece.
Total momentum after collision = Total momentum before collision. Initially 1kg was at rest.
$\vec{P_{1}} + \vec{P_{2}} + \vec{P_{3}} = 0$
$\vec{P_{3}} = (\vec{P_{1}} + \vec{P_{2}})$
Magnitude of $P_{3} = \sqrt{P_{1}^{2} + P_{2}^{2}}$
$= \sqrt{6^{2} + 6^{2}} = \sqrt{72} = 6 \sqrt{2} k g m s^{- 1}$
$3 m v = 6 \sqrt{2}$
$v = \frac{6 \sqrt{2}}{3 \times (\frac{1}{5})} = 10 \sqrt{2}$
$= 14.14 m s^{- 1}$

Updated on:21/07/2023