Two masses m1 and m2 are attached to two ends of a massless string passing over a frictionless massless pulley and m2 is placed on an inclined plane. Assuming that the friction between the mass m2 and the plane is zero find the acceleration of the masses and the tension in the string if m1=20.5kg,m2=10.5kg and θ=45∘.
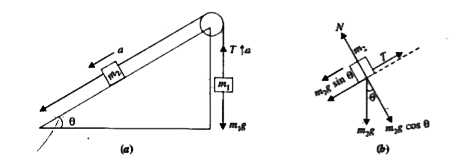
The forces acting on the mass m1 are its weight m1 g acting vertically downwards and the tension in the string T acting vertically upwards. The mass m1 accelerates vertically upwards. Applying Newton.s second law to the mass m1,
T−m1g=m1a ......(i)
The weight of m2g acting vertically downwards. It is resolved into two components, the components m2gcosθ balances the normal reaction N. m2gsinθ is parallel to the plane and is opposite to the tension T. If a is the acceleration of the mass m2. We have,
m2gsinθ−T=m2a ........(ii)
m2gcosθ=N ............(iii)
Adding equations (i) and (ii)
T−m1g+m2gsinθ−T=m1a+m2a
a=m2gsinθ−m1gm1+m2 ..........(iv)
Substituting then value of a in equation (i)
T=m1a+m1g=m1m2gsinθ−m21gm1+m2+m1g
T=m1m2g(1+sinθ)m1+m2 ...........(v)
Given m1=20.5kg,m2=10.5kg,θ=45∘
a=?,T=?
From equation (iv) we have,
a=10.5×9.8sin45−20.5×9.820.5+10.5=4.13m/s2
Substituting the value of a, and m1 in equation (i)
T=m1g+m1a=m1(a+g)=20.5(−4.13+9.8)=116.23N.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
20 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS
93 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
Two mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

View SolutionTwo mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

View Solution
Knowledge Check
Two masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
 A20m/s2B5m/s2C2.5m/s2D10m/s2
A20m/s2B5m/s2C2.5m/s2D10m/s2Two masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
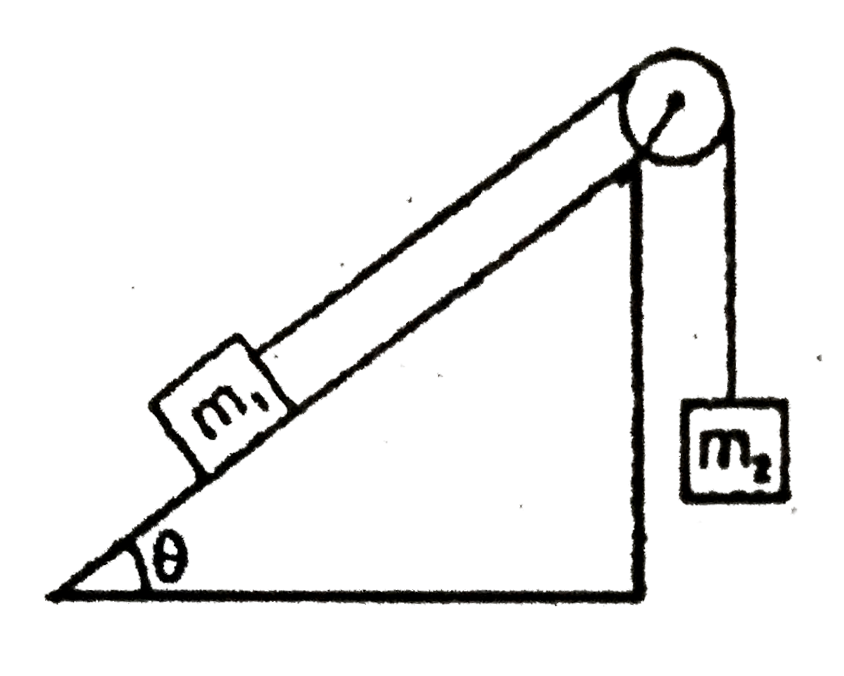
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?AzeroB(2/3)ms−2C5ms−2D10/3ms−2Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Two masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2

if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
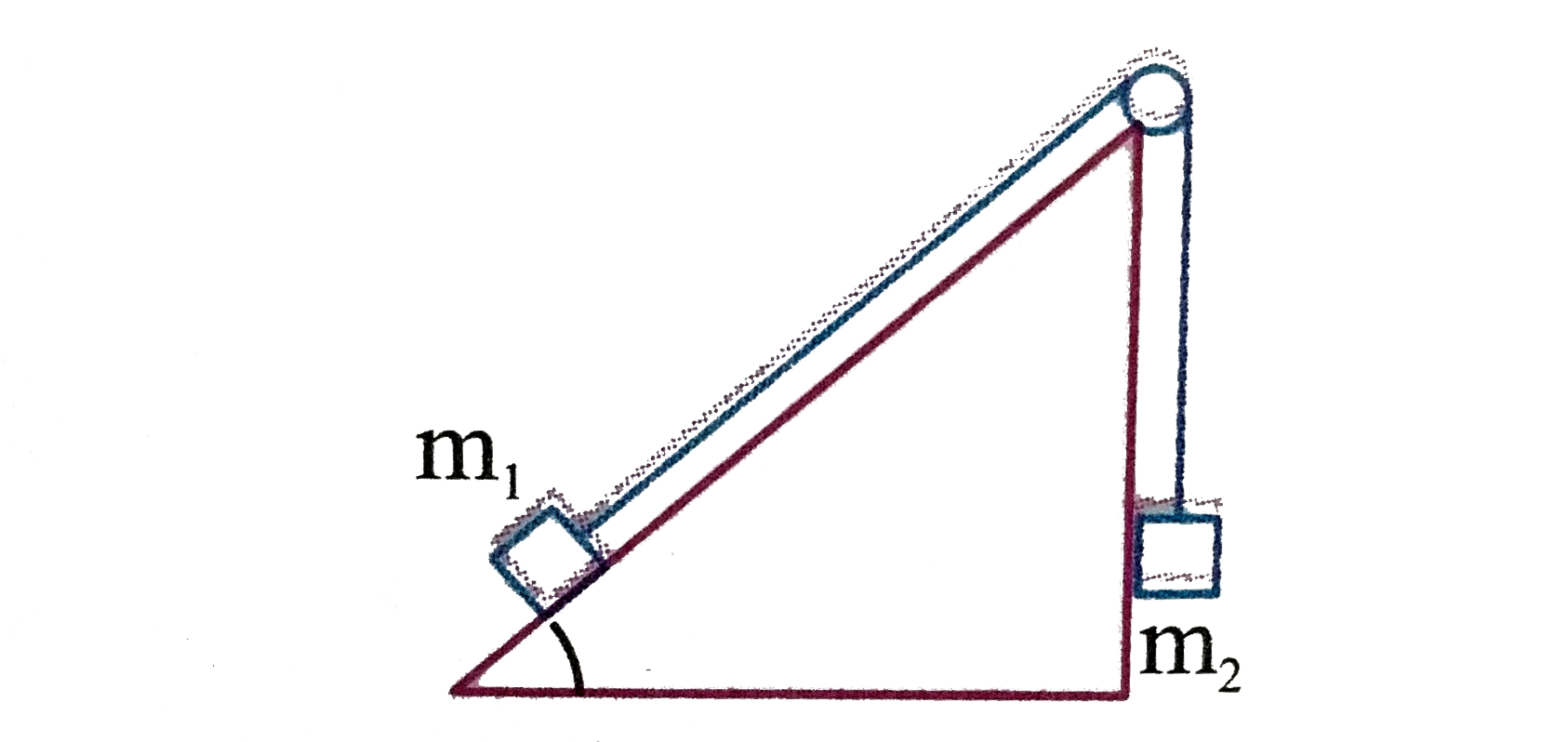
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.

View Solution
