The poteintial energy function for a particle executing linear simple harmonic motion is given by V(x)=12Kx2, where K is the force constant of the oscillator. For K=12Nm−1. The praph of V (x) versus x is shown in Fig. 4.4.44. Show that a particle of total energy 1J moving under this potential must ''turn back'' when it reaches x=±2m.
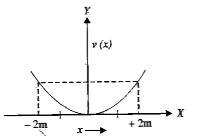
Maximum P.E. =12×12×22=1J. This is total energy. So the particle must turn back when x=±2m because its P.E. cannot be greater than the total energy.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SELECTED PROBLEMS
249 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
20 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View Solution
Knowledge Check
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
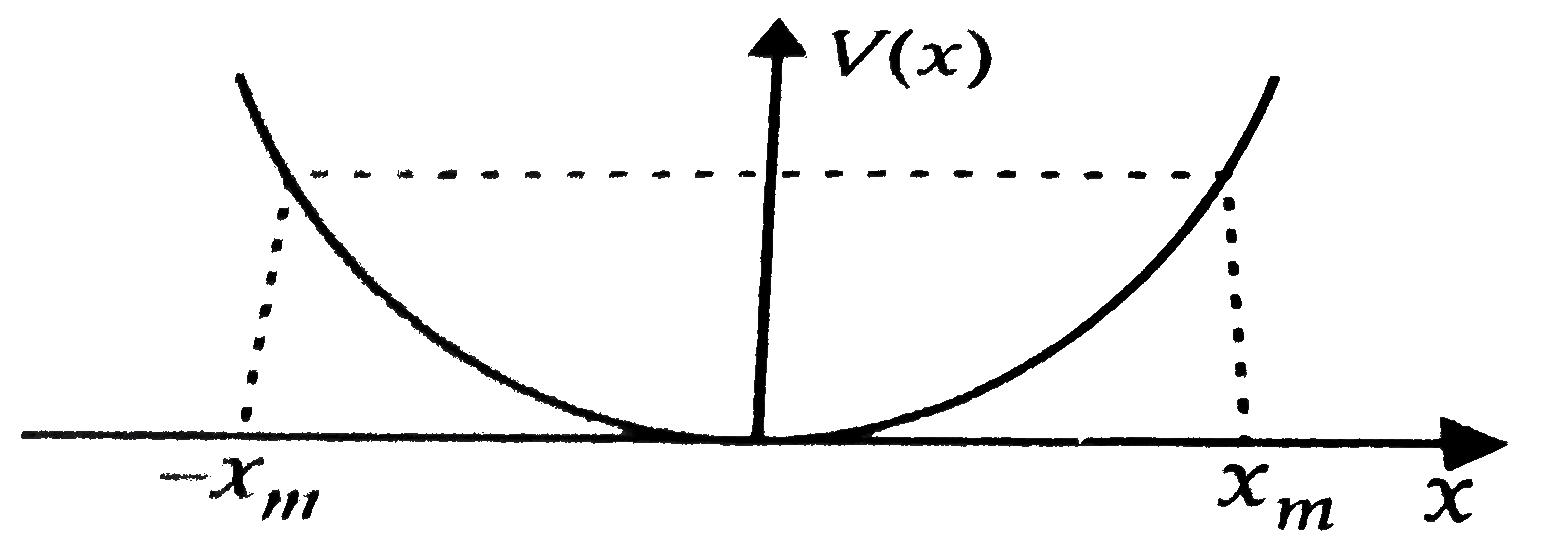 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt EThe potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt EThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
A−3kB+3kCkDNone of these
The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionThe energy of a particle executing simple harmonic motion is given by E=Ax2+Bv2 where x is the displacement from mean position x=0 and v is the velocity of the particle at x then choose the correct statement(s)
View SolutionThe potential energy of a 1kg particle free to move along the x-axis is given by V(x)=(x44−x22)J The total mechanical energy of the particle is 2J then the maximum speed (∈m/s) is
View SolutionThe potential energy of a particle with displacement X is U(X). The motion is simple harmonic, when (K is a positive constant)
View Solution
