A door has a mass of 25kg, height 2 m and width of 0.90m. One hinge is filtres at a distance 0.25m from the bottom. Each hinge supports half the door's weight. Assume that the centre of gravity of the door is its geometric centre, find
The horizontal force components exerted by each hinge on the door.
W×0.45=F1×1.5,F1=73.5N.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES43videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS60videos
DYNAMICS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
Similar Questions
A uniform 8 kg door with dimensions 75cm×200cm is pivoted at hinges 25cm from the top and from the bottom.The horizontal force exerted by each hinge is 10aN .The value of a is? (Assume centre of mass of gate at its geometrical centre)
View SolutionA uniform wood door has mass m, height h, and width w. It is hanging from two hinges attached to one side , the hinges are located h/3 and 2h/3 form the bottom of the door. Suppose that m=20kg,h=2.20m, and the bottom smooth hinge is not screwed into the door frame. Find the forces acting on the door.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
As shown in figure, the hinges A and B hold a uniform 400N door in place. The upper hinge supports the entire weight of the door. Find the resultant force exerted on the door at the hinges, the width of the door is h2, where h is the distance between the hinges.
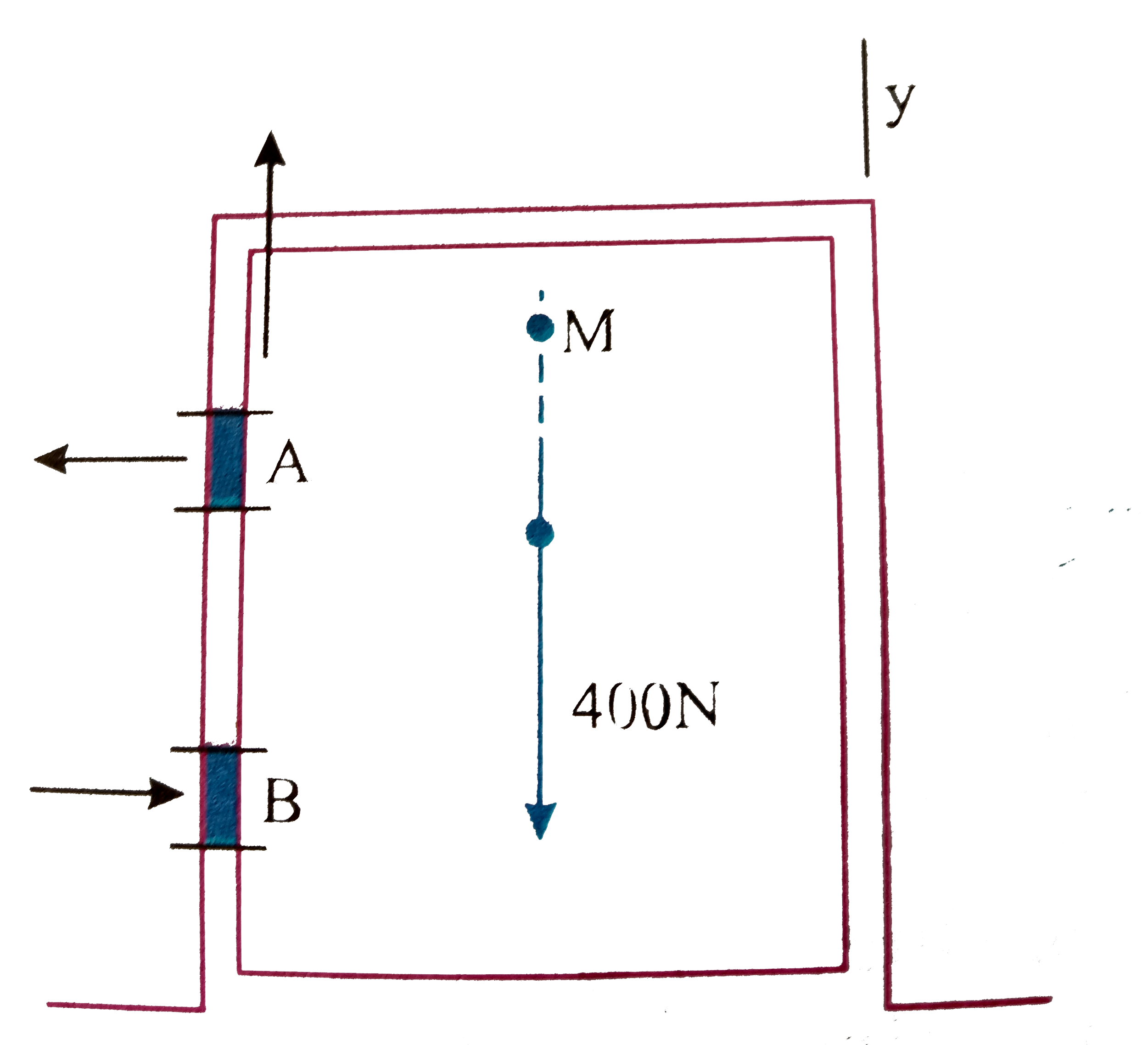 A312NB280NC412ND480N
A312NB280NC412ND480N - Question 2 - Select One
The figure shows the top view of a door that is 2 m wide. Two forces are applied to the door as indicated. What is the magnitude of the net torque on the door with respect to the hinge?
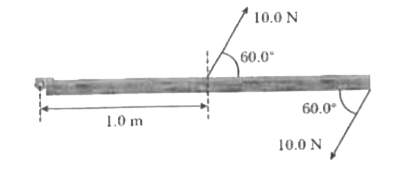 A0N⋅mB10.0N⋅mC5.0N⋅mD8.7N⋅m
A0N⋅mB10.0N⋅mC5.0N⋅mD8.7N⋅m - Question 3 - Select One
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
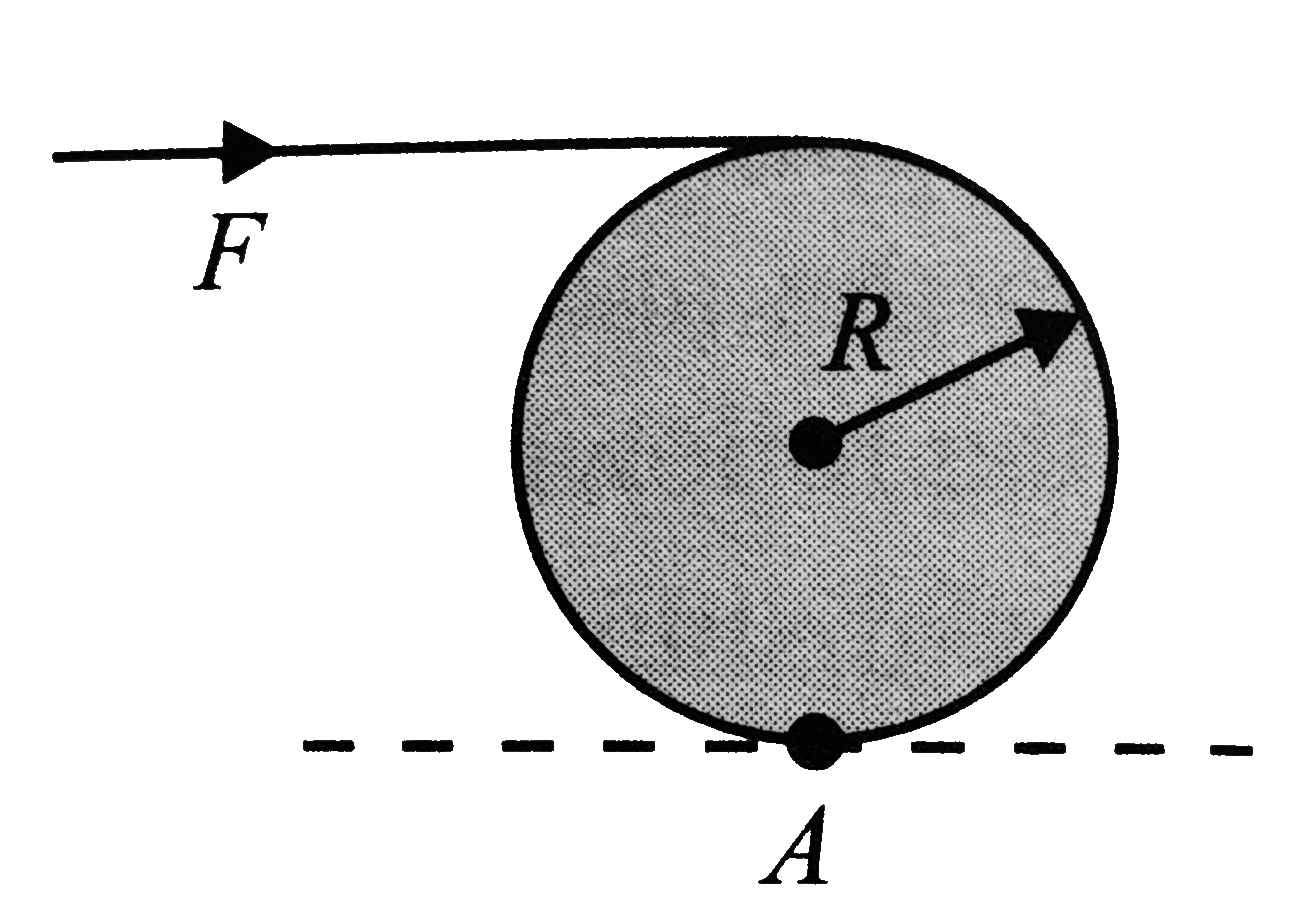
Component of reaction at the hinge in the horizontal direction isAF4BFCF3DF2
the door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View Solutionthe door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View Solutionthe door of an almirah is 6 ft high, 1.5 ft wide and weights 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitude of the forces exerted by the hinges on the door are equal find this magnitude.
View SolutionA uniform wood panel of mass 35.0 kg is hinged ver tically on a wall by two hinges, one 0.300 m from its top and the other 0.300 m from its bottom. The panel is 2.10 m tall and 0.910 m wide. A y axis extends upward through the hinges and an x axis extends outward along the panel's width. If each hinge supports half the panel's weight, what are the forces on the panel at (a) the top hinge and (b) the bottom hinge, both in unit-vec notation?
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.

Component of reaction at the hinge in the horizontal direction isView Solution

