A man weighing 50kg walks along a rope tied between two pegs which are 20 m apart horizontally. When he comes to the middle point of the rope it sage by 0.875m. Calculate the tention in the string.
Let T be the tension in each part of the string.
50/sin(180−2θ)=T/sin(90+θ)
tanθ=0.875/10=0.0875,θ=5∘
T=50cos5/sin10=293kgwt.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES
43 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
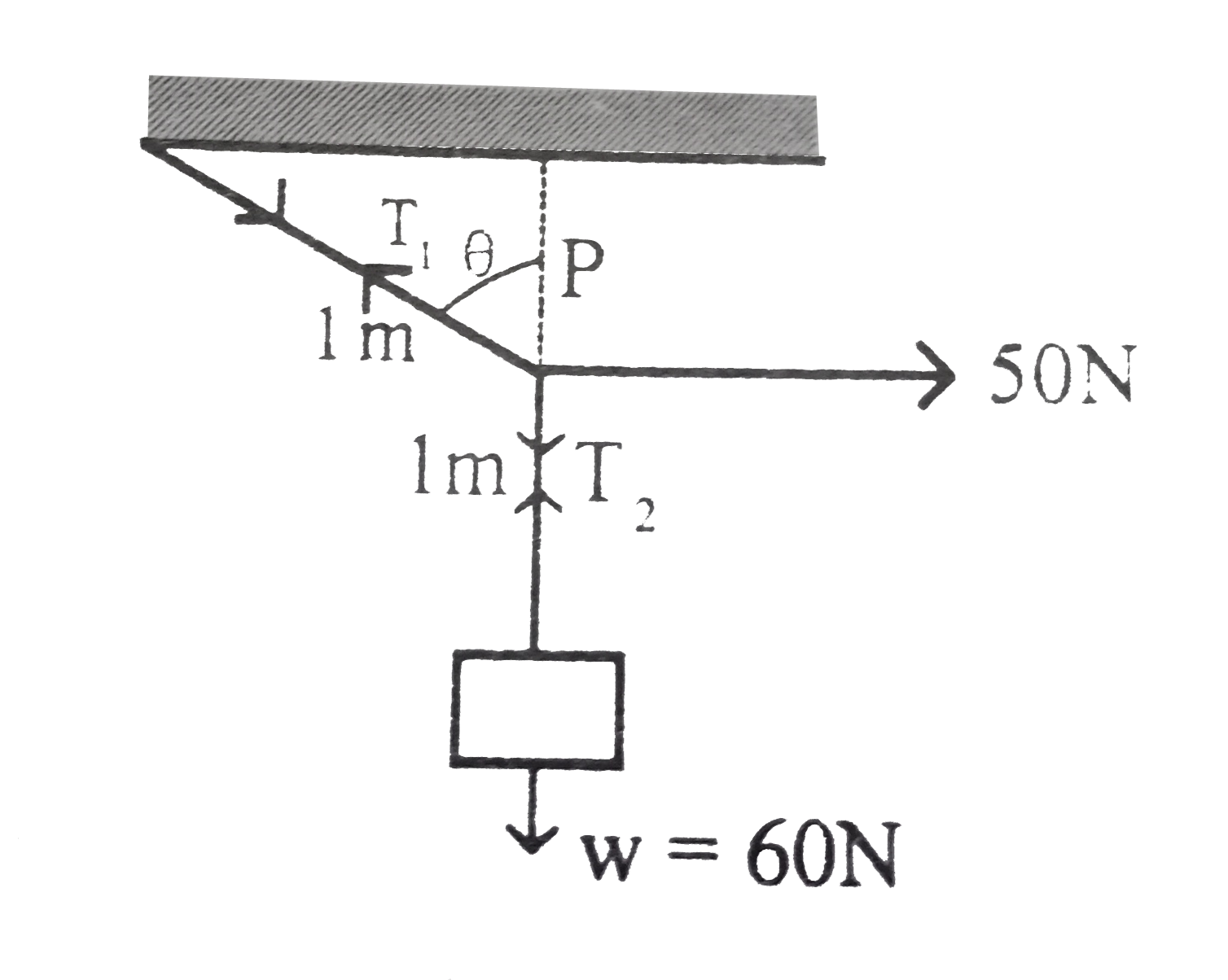
View SolutionA man of 80 kg fastns a rope to a mass of 120kg, and passes the rope over a smooth pulley. In order to raise it up he climbs the riope with acceleration 3g2 relative to the rope. Calculate the tension in the rope in N. (Take g=10m/s2)
View Solution
Knowledge Check
A mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
 Atan−1(45)Btan−1(54)Ctan−1(56)DNone of these
Atan−1(45)Btan−1(54)Ctan−1(56)DNone of theseA mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
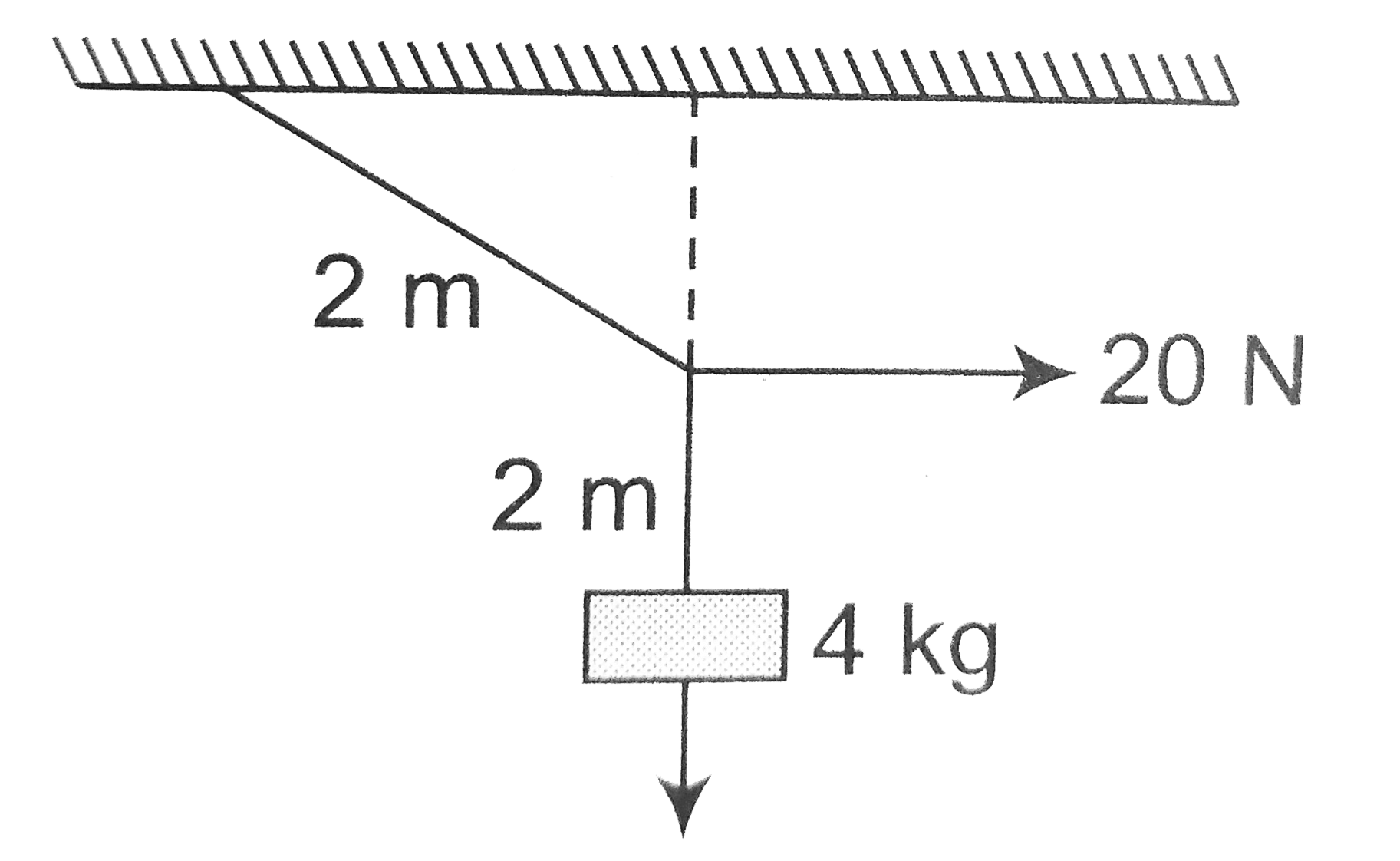 Atan−12Btan−1(12)Ctan−1√2Dtan−1(1)(√2)
Atan−12Btan−1(12)Ctan−1√2Dtan−1(1)(√2)A rope of mass 5 kg is hanging between two supports as shown. The tension at the lowest point of the rope is close to (take g = 10m/s2)
 A22 NB44 NC28 ND14 N
A22 NB44 NC28 ND14 N
A mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View SolutionA mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View SolutionOne end of a long rope is tied to a fixed vertical pole. The rope is stretched horizontally with a tension 8 N. Let us consider the length of the rope to be along X-axis. A sample harmonic oscillator at x = 0 generates a transverse wave of frequency 100 Hz and amplitude 2 cm along the rope. Mass of a unit length of the rope is 20 gm/m. Ignoring the effect of gravity, answer the following questions
Wavelength of the wave is
View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
View SolutionA mass of 10 kg is suspended vertically by a rope of length 2 m from a ceiling. A force of 60 N is applied at the middle point of the rope in the horizontal direction, as shown in Fig. Calculate the angle the rope makes with the vertical. Neglect the mass of the rope and take g=10ms−2.

View Solution
