There is a regular octagon A B C D E F G H, a frog is at the vertex A. It can jump on to any of the vertices except the exactly opposite vertex. The frog visits all the vertices exactly once and then reaches vertex E then how many times did it jump before reaching E?
7
2n+1
6
Can’t be determined
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
Let A and D be opposite vertices of a square. A frog starts jumping at vertex A. From any vertex of the square except D, it may jump to either of the two adjacent vertices. When it reaches D, the from stop and stays there. The number of distinct path of exactly 6 jumps ending at D are ____________________
View SolutionIn the given triangle, name the following:
(a). The vertices of the triangle
(b). The sides of the triangle
(c) the side opposite to vertex Q
(d) the vertex opposite to side PQ
(e) the three angles using three letters
(f) the three angles using a single letter
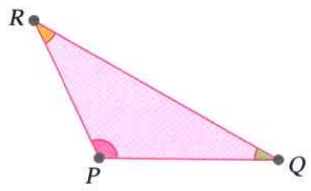
View Solution
Knowledge Check
A, B, C, D, E, F in that order, are the vertices of a regular hexagon with centre orgin. If the position vectors of the vertices A and B are respectively, 4ˆi+3ˆj−ˆkand−3ˆi+ˆj+ˆk, then DE is equal to
A7ˆi+2ˆj−2ˆkB−7ˆi−2ˆj+2ˆkC3ˆi−ˆj−ˆkD−4ˆi−3ˆj+2ˆkA, B, C, D, E, F in that order, are the vertices of a regular hexagon with centre orgin. If the position vectors of the vertices A and B are respectively, 4ˆi+3ˆj−ˆkand−3ˆi+ˆj+ˆk, then DE is equal to
A7ˆi+2ˆj−2ˆkB−7ˆi−2ˆj+2ˆkC3ˆi−ˆj−ˆkD−4ˆi−3ˆj+2ˆk
Eight persons A, B, C, D, E, F, G and H are sitting around a rectangular table in such a way that two persons sit on each of the four sides of the table, facing the centre. Persons sitting on opposite sides are exactly opposite to each other. D faces North and sits exactly opposite H. E is in the immediate left of H. A and G sit on the same side. G is exactly opposite of B, who is on the immediate right of C. A is to the immediate left of D.
Which of the following statements is definitely true?
1) A is facing North.
2) E is sitting opposite F.
3) F is on the immediate left of G.
4) C is on the immediate left of A.
5) None of these
View SolutionEight persons A, B, C, D, E, F, G and H are sitting around a rectangular table in such a way that two persons sit on each of the four sides of the table, facing the centre. Persons sitting on opposite sides are exactly opposite to each other. D faces North and sits exactly opposite H. E is in the immediate left of H. A and G sit on the same side. G is exactly opposite of B, who is on the immediate right of C. A is to the immediate left of D.
Who is next to E in clockwise direction?
1) G
2) B
3) F
4) A or F
5) None of these
View SolutionEight persons A, B, C, D, E, F, G and H are sitting around a rectangular table in such a way that two persons sit on each of the four sides of the table, facing the centre. Persons sitting on opposite sides are exactly opposite to each other. D faces North and sits exactly opposite H. E is in the immediate left of H. A and G sit on the same side. G is exactly opposite of B, who is on the immediate right of C. A is to the immediate left of D.
Who is sitting opposite E?
1) D
2) A
3) F
4) A or D
5) None of these
View SolutionEight persons A, B, C, D, E, F, G and H are sitting around a rectangular table in such a way that two persons sit on each of the four sides of the table, facing the centre. Persons sitting on opposite sides are exactly opposite to each other. D faces North and sits exactly opposite H. E is in the immediate left of H. A and G sit on the same side. G is exactly opposite of B, who is on the immediate right of C. A is to the immediate left of D.
Who is sitting opposite A?
1) G
2) D
3) E
4) C
5) None of these
View SolutionEight persons A, B, C, D, E, F, G and H are sitting around a rectangular table in such a way that two persons sit on each of the four sides of the table, facing the centre. Persons sitting on opposite sides are exactly opposite to each other. D faces North and sits exactly opposite H. E is in the immediate left of H. A and G sit on the same side. G is exactly opposite of B, who is on the immediate right of C. A is to the immediate left of D.
Which of the following pairs of persons has both the persons sitting on the same side with the first person sitting on the right of the second person?
1) DF
2) CB
3) FC
4) AG
5) None of these
View SolutionThree vertices of a triangle are A(1,2),B(−3,6)andC(5,4). If D, E and F are the mid-points of the sides opposite to the vertices A, B and C, respectively, show that the area of triangle ABC is four times the area of triangle DEF.
View Solution
