Question

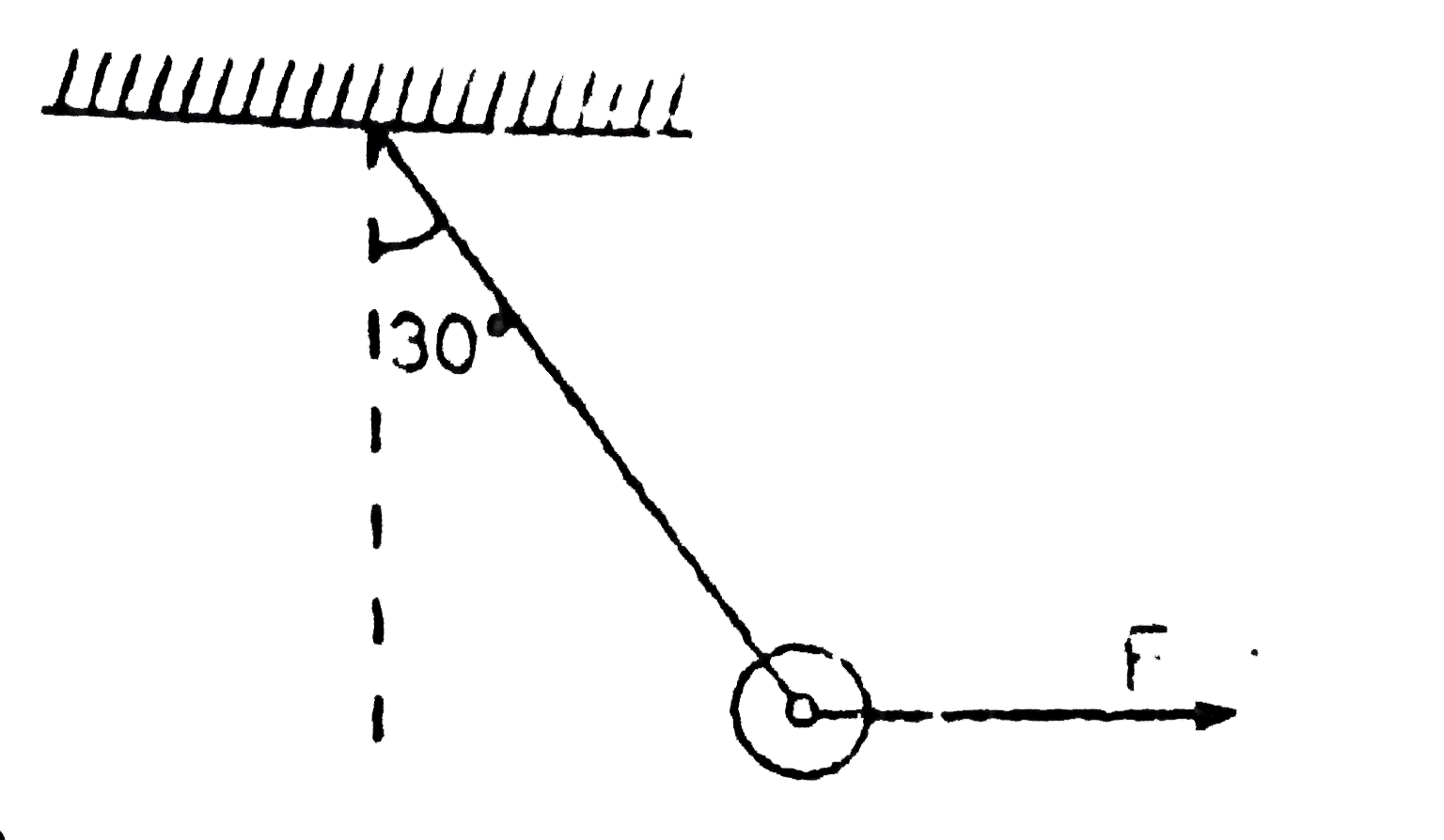
A block of mass 2 kg is suspended by a weightless string of length 1 m. A horizontal force is applied to displace the block slowly until the string makes an angle of ${30}^{\circ }$ with the initial vertical direction. What is the work done by the applied force? (Take $g=10m/s^2$)

Options

A. `20(1-(sqrt(3))/(2))J`
B. `(5sqrt(3))/(2)J`
C. 10 J
D. 20 J

Answer

A

Explanation

To solve the problem, we need to find the work done by the applied force when the block is displaced to make an angle of $${30}^{\circ }$$ with the vertical.

1. Identify the Given Values:
- Mass of the block, \(m = 2 \, \text{kg}\)
- Length of the string, \(L = 1 \, \text{m}\)
- Angle with the vertical, \(\theta = 30^\circ\)
- Acceleration due to gravity, \(g = 10 \, \text{m/s}^2\)

2. Calculate the Height Change:
When the block is displaced, the vertical height \(h\) it rises can be calculated using the formula:
\( h = L - L \cos(\theta) \)
Substituting the values:
\( h = 1 - 1 \cdot \cos(30^\circ) \)
We know that \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\):
\( h = 1 - 1 \cdot \frac{\sqrt{3}}{2} = 1 - \frac{\sqrt{3}}{2} \)

3. Calculate the Work Done Against Gravity:
The work done against gravity when the block rises to height \(h\) is given by:
\( W_g = mgh \)
Substituting the values:
\( W_g = 2 \cdot 10 \cdot h = 20h \)
Now substituting \(h\):
\( W_g = 20 \left(1 - \frac{\sqrt{3}}{2}\right) \)

4. Calculate the Numerical Value of Work Done:
To find the numerical value of \(W_g\):
\( W_g = 20 \left(1 - \frac{\sqrt{3}}{2}\right) = 20 \left(1 - 0.866\right) \approx 20 \cdot 0.134 \approx 2.68 \, \text{J} \)

5. Determine Work Done by the Applied Force:
Since the block is displaced slowly, the work done by the applied force is equal to the work done against gravity:
\( W_{\text{applied}} = W_g = 20 \left(1 - \frac{\sqrt{3}}{2}\right) \approx 2.68 \, \text{J} \)

Final Answer:
The work done by the applied force is approximately \(2.68 \, \text{J}\).