Centre of mass of semi circular disc by two unique methods.
Step by step video solution for Centre of mass of semi circular disc by two unique methods. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A circular disc of radius R is removed from a bigger circular disc of radius 2R, such that the circumference of the disc coincides. The centre of mass of the new disc is αR from the centre of bigger disc. The value of alpha is
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
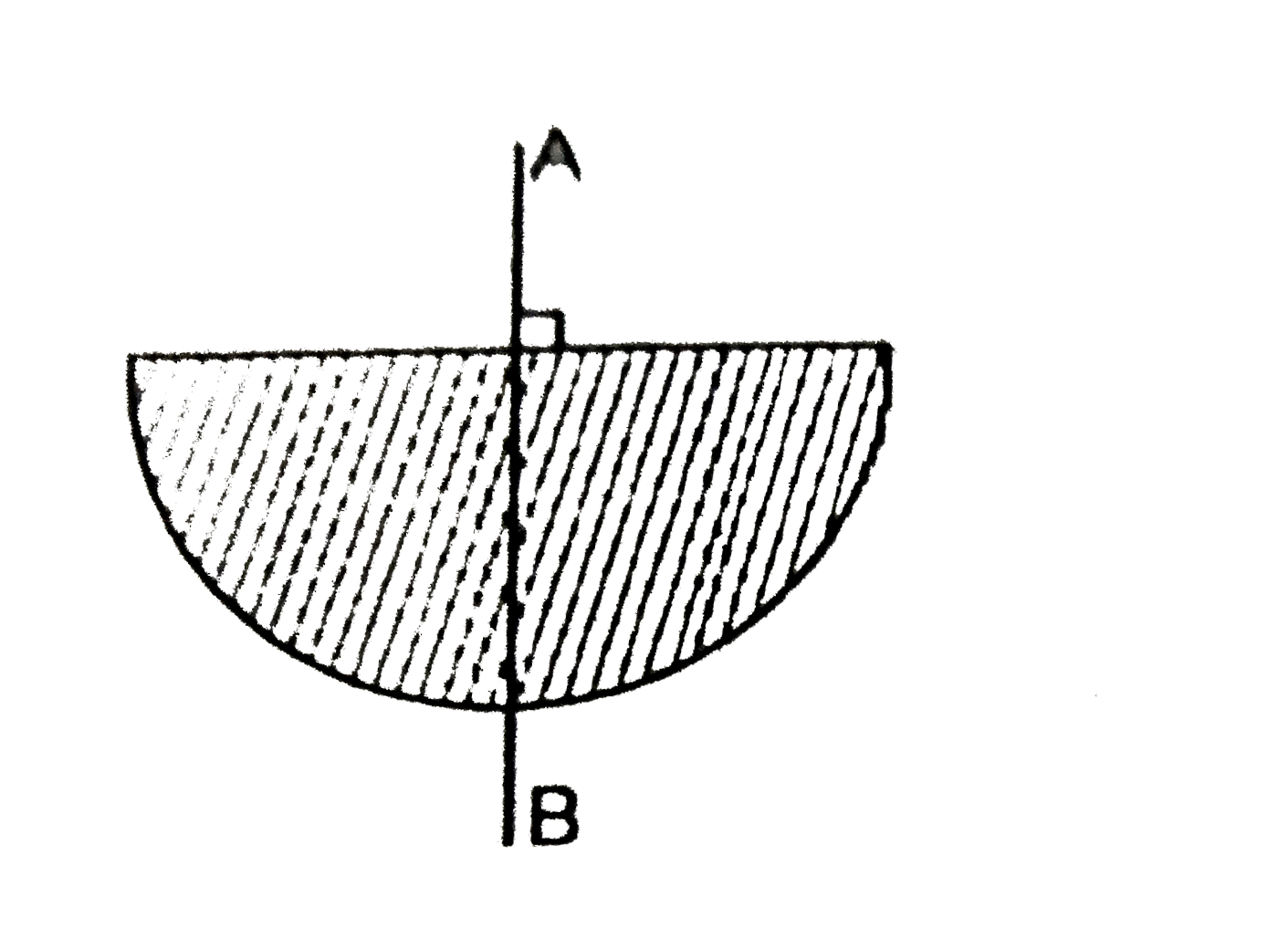
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is alphaR from the centre of the bigger disc . the value of alpha is
View SolutionCbse | Centre Of Mass Of Rod | Centre Of Mass Of Semi Circular Ring | Centre Of Mass Of Half Disc
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the disc coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of α is :
View SolutionThe moment of inertia of a uniform semi circular disc of mass M and radius .r. about a line perpendicular to the plane of disc through the centre is:
View SolutionA circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View Solution
