The maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
√gl
√3gl
√5gl
√7gl
The correct Answer is:C
vmin=√5gl
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (HORIZONTAL PROJECTILE MOTION)11videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (OBLIQUE PROJECTILE MOTION)47videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON19videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - ASSERTION AND REASON24videos
MOTION IN ONE DIMENSION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
Similar Questions
One end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Assertion For looping a verticla loop of radius, r the minimum velocity at lowest point should be √5gr. Reason In this event the velocityh at the highest point will be zero.
ABoth assertion and reson are true and reason is the correct explanation of assertionBBoth assetion and reason are true but reason is not the correct explanation of assertionCAssertion is true but reason is falseDBoth assetion and reason are flase - Question 2 - Select One
A particle is projected so as to just move along a vertical circle of radius r. The ratio of the tension in the string when the particle is at the lowest and highest point on the circle is -
A1Bfinite but largeCzeroDInfinite - Question 3 - Select One or More
A horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
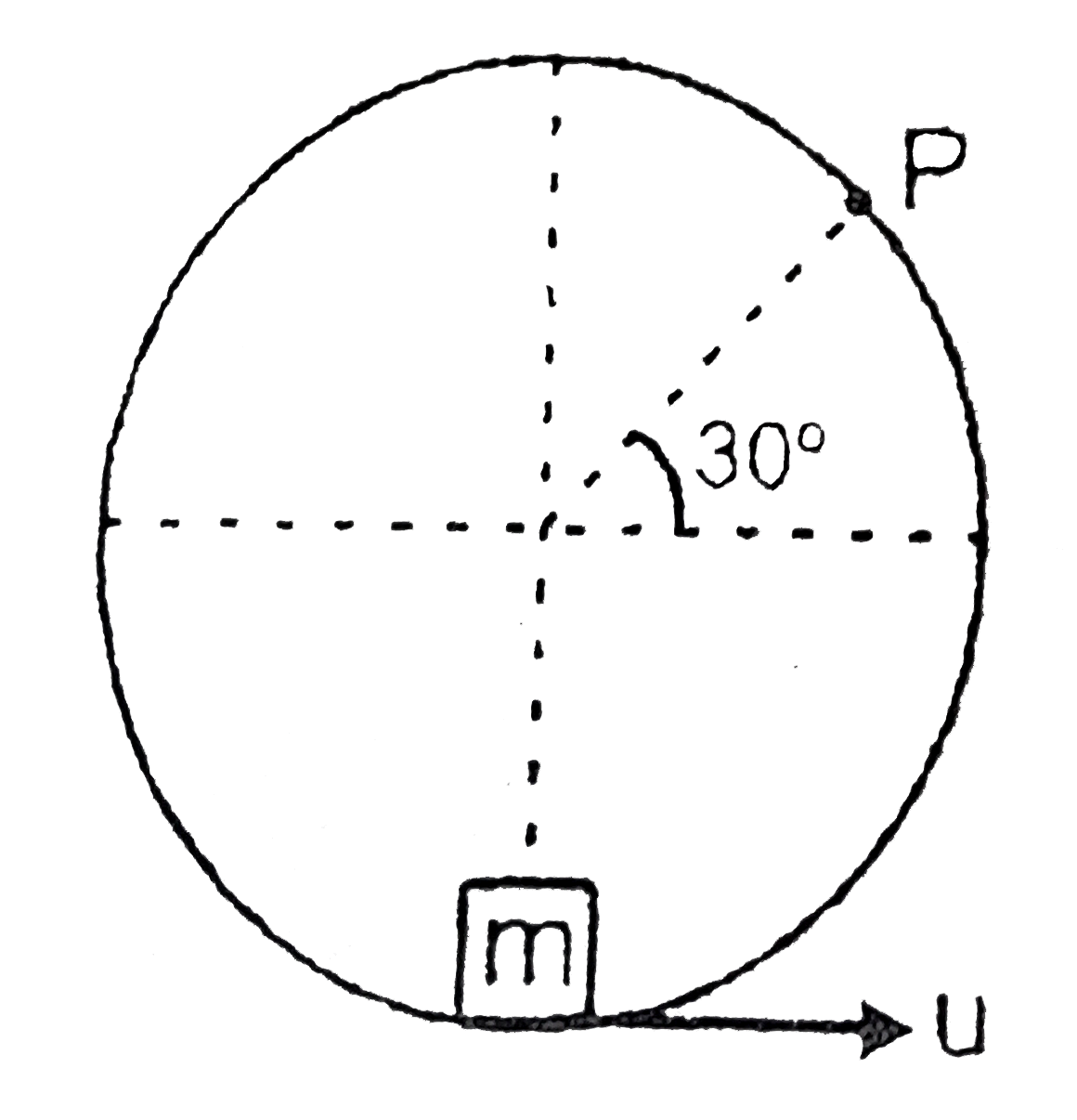 AIf the block moves anti clockwise then u=√3.5gRBIf the block moves anti clockwise then u=√3gRCIf the block moves clockwise then u=√3.5gRDIf the block moves clockwise then u=√5gR
AIf the block moves anti clockwise then u=√3.5gRBIf the block moves anti clockwise then u=√3gRCIf the block moves clockwise then u=√3.5gRDIf the block moves clockwise then u=√5gR
A stone of mass 100 g attached to a string of length 50 cm is whirled in a vertical circle by giving it a velocity of 7 m/s at the lowest point. Find the velocity at the highest point .
View SolutionA body of mass 0.4 kg is tied to one end of a string and the other end of the string is tied to a small pivot on a vertical wall . Calculate the minimum speed of the body required at its lower most pint to avoid slacking of string at any point in its motion along the vertical circle of radius 1 m .
View SolutionA stone is tied to one end of a string and rotated in a vertical circle . What is the difference in tensions of the string at lowest and highest points of the vertical circle ?
View SolutionA stone of mass 0.4 kg is tied to a string and rotated in a vertical circle of radius 1.2 m . Calculate the speed of the stone for which the tension in the string is zero at the highest point of the circle . What is the tension at the lowest point in this case ?
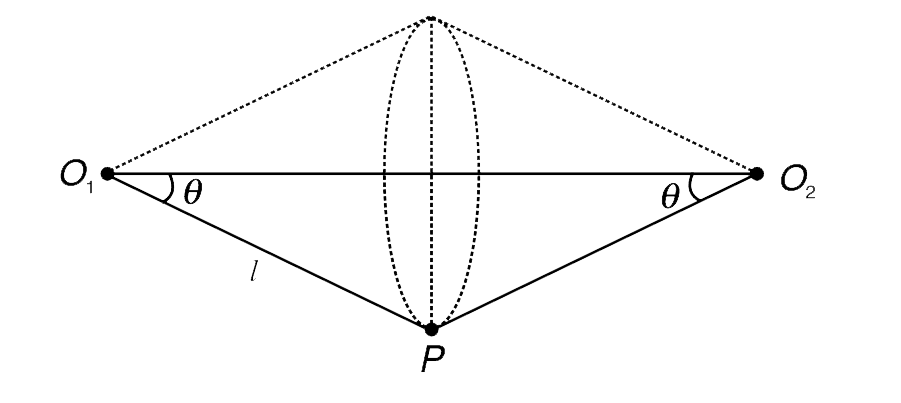
View SolutionA particle P is attached to two fixed points O1 and O2 in a horizontal line, by means of two ight inextensible strings of equal length l. It is projected with a velocity just sufficient to make it describe a circle, in a vertical plane, without the strings getting slack and with the angle<O2O1P=<O1O2P=θ. When the particle is at its lowest point, the string O2P breaks and the subsequent path of the particle was found to be a circle of radius l cosθ. Find θ.
 View Solution
View Solution

