Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
v√m2k
m√v2k
√mvk
mv2k
The correct Answer is:A
Law of conservation of momentum –
mv = (m + m)v.
⇒v.=v2
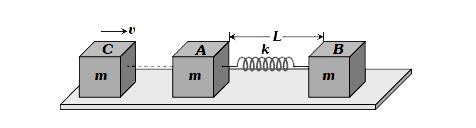
Law of conservation of energy –
(KE)C=(KE)system+(PE)system
⇒12mv2=12(2m)(v.)2+12kx2
⇒kx2=mv2−mv22=12mv2
⇒x=v√m2k
Topper's Solved these Questions
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Power)
18 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Elastic and Inelastic Collision)
44 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Work Done by Variable Force)
26 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON
25 Videos
Similar Questions
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View Solution
Knowledge Check
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)Two blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)
Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
Two blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
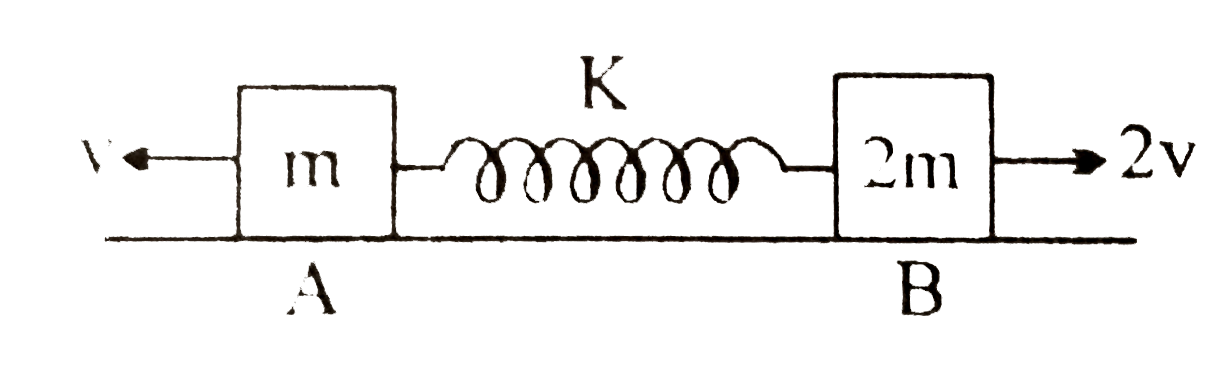
View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

View Solution
