A solid sphere rolls without slipping, first horizontal and then up to a point X at height h on an inclined plane before rolling down, as shown.

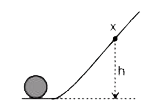
The initial horizontal speed of the sphere is

A

$\sqrt{\frac{10 g h}{7}}$

B

$\sqrt{\frac{7 g h}{5}}$

C

$\sqrt{\frac{5 g h}{7}}$

D

$\sqrt{2 g h}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$m g h = \frac{1}{2} m v^{2} + \frac{1}{2} \frac{2}{5} m R^{2} \frac{v^{2}}{R^{2}} \Rightarrow m g h = \frac{7}{10} m v^{2}$
$\Rightarrow v = \sqrt{\frac{10 g h}{7}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid sphere rolls down without slipping from rest on a $30^{\circ}$ incline. Its linear acceleration is
A $5 g / 7$
B $5 g / 14$
C $2 g / 3$
D $g / 3$
Question 2 - Select One
A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

AThe acceleration of the centre of the sphere is $9.8 m / s^{2}$
BThe acceleration of the centre of the sphere is $10 m / s^{2}$
CThe direction of frictional force on the sphere is towards right
DThe value of frictional force is 3N
Question 3 - Select One
A solid sphere rolls down two different inclined planes of the same height but of different inclinations
AIn both cases the final speeds and time of descent will be same
BThe final speeds will be same but time of descent will be different
CThe final speed will be different but time of descent will be same
DThe final speeds and time of descent both will be same

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Rolling on Inclined Plane)

Home
Ask Doubt
Profile