A solid sphere spinning about a horizontal axis with an angular velocity $ω$ is placed on a horizontal surface. Subsequently it rolls without slipping with an angular velocity of :

A

$\frac{2 ω}{5}$

B

$\frac{7 ω}{5}$

C

$\frac{2 ω}{7}$

D

$ω$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Initial sphere is slipping and finally it starts rolling during its motion $τ$ about point of contact is zero. Angular momentum of sphere about point of contact remains conserved

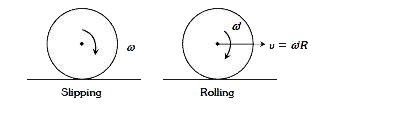
$I ω = (I + M R^{2}) ω .$
$\Rightarrow \frac{2}{5} M R^{2} ω = (\frac{2}{5} M R^{2} + M R^{2}) ω \Rightarrow ω . = \frac{2 ω}{7}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid sphere with a velocity (of centre of mass) $v$ and angular velocity $ω$ is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of $v$ )
Bmust be backward (opposite to $v$ )
Ccannot be zero
Dnone of the above
Question 2 - Select One
A hoop of radius r and mass m rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
A $\frac{r ω_{0}}{4}$
B $\frac{r ω_{0}}{3}$
C $\frac{r ω_{0}}{2}$
D $r ω_{0}$
Question 3 - Select One
A hoop of radius $r$ mass $m$ rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
A $\frac{r ω_{0}}{2}$
B $r ω_{0}$
C $\frac{r ω_{0}}{4}$
D $\frac{r ω_{0}}{3}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Rolling on Inclined Plane)

Home
Ask Doubt
Profile