From a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
1/2M(R2+r2)
1/2M(R2−r2)
1/2M(R4+r4)
1/2M(R4−r4)
The correct Answer is:A
Area of the face of ring = π(R2−r2)
Mass per unit area = Mπ(R2−r2)
Face area of ring of radius x and x+dx=2πxdx
Mass (dm) of this ring = Mπ(R2−r2)×2πxdx
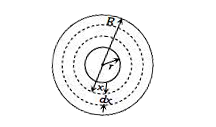
MOI of this ring -
implies I=∫x2dm=∫Rrx2.2M(R2−r2)xdx
implies I=2M(R2−r2)[x44]Rr
implies I=2M4(R2−r2)[R4−r4]=M2(R2+r2)
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)52videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)44videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)34videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason15videos
SIMPLE HARMONIC MOTION
Similar Questions
Find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
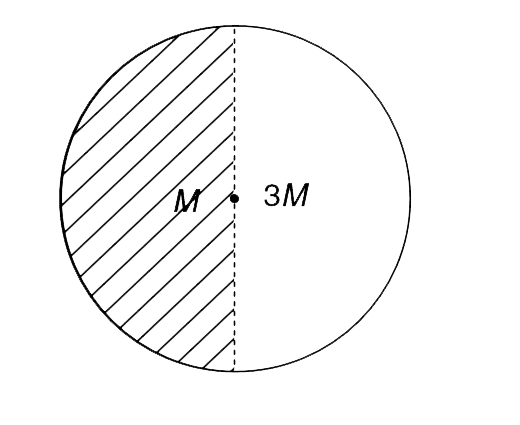
View SolutionTwo uniform semicircular discs, each of radius R, are stuck together to form a disc. Masses of the two semicircular parts are M and 3M. Find the moment of inertia of the circular disc about an axis perpendicular to its plane and passing through its centre of mass.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
A6 IB4 IC2 ID8 I - Question 2 - Select One
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3 - Question 3 - Select One
A rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
Am[r2−lb6πr2(l2+b2)Bm2[r2−lb6πr2(l2+b2)]Cm2[r2−(l2+b2)6]Dnot determinable as mass of the rectangular piece is not given
The moment of inertia of a solid sphere of radius R about an axis passing through its diameter is I. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionMoment of inertia of a thin circular plate of mass M, radius R about an axis passing through its diameter is I. The moment of inertia of a circular ring of mass M, radius R about an axis perpendicular to its plane and passing through its centre is
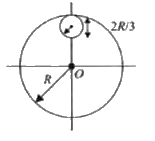
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 View Solution
View Solution

