Seven identical coins are rigidly arranged on a flat table in the pattern shown below so that each coin touches its neighbors. Each coin is a thin disc of mass m and radius r. Note that the moment of inertia of an individual coin about an axis passing through centre and perpendicular to the plane of the coin is $m^{2} / 2$

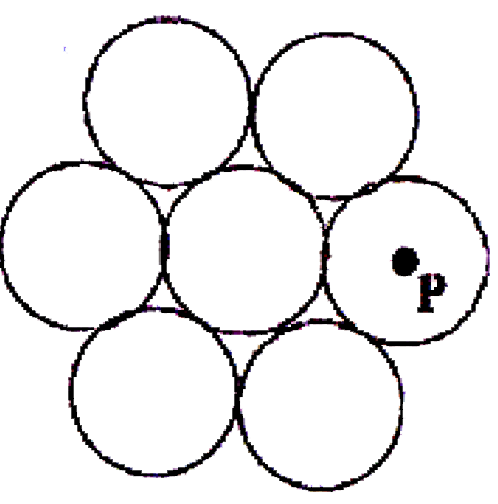
The moment of inertia of the system of seven coins about an axis that passes through the point P (the centre of the coin positioned directly to the right of the central coin) and perpendicular to the plane of the coins is–

A

$\frac{55}{2} m r^{2}$

B

$\frac{127}{2} m r^{2}$

C

$\frac{111}{2} m r^{2}$

D

$55 m r^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$I_{p} = \frac{m r^{2}}{2} + 3 [\frac{m r^{2}}{2} + m {(2 r)}^{2}] + [\frac{m r^{2}}{2} + m {(r 2 \sqrt{3})}^{2}]$

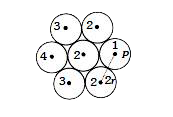
$\times 2 + [\frac{m r^{2}}{2} + {(4 r)}^{2} m]$
$= \frac{111}{2} m r^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increased
Bchanges if its axis of rotation is changed
Cincreases if its angular velocity is increased
Dboth (a) and (b) are correct
Question 2 - Select One
The moment of inertia of a circular disc about an axis passing through its centre and perpendicular to the plane is $4 k g m^{2}$ . Its moment of inertia about the diameter is
A $2 k g m^{2}$
B $6 k g m^{2}$
C $4 k g m^{2}$
D $8 k g m^{2}$
Question 3 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)

Home
Ask Doubt
Profile