A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
→E=λ4πε0a(−ˆi)
→E=λ4πε0a(−ˆi)
→E=λ2πε0a(−ˆi)
→E=λ2eπε0a(−ˆi)
The correct Answer is:A

Charge on dx is dq=λdx
Electric field due to element dx
dE=dq4πε0x2⇒E=∫∞aλdx4πε0x2
⇒E=λ4πε0[x−2+1−2+1]∞a=λ4πε0a⇒→E=λ4πε0a(−ˆi)
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)21videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Flux and Gauss.s Law)27videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION & REASON25videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason26videos
ELECTRONICS
- BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON18videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
A continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
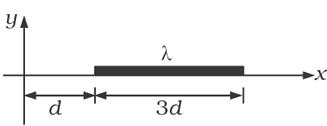 View Solution
View SolutionA straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
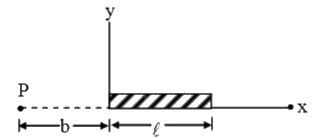 Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzero
Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzero - Question 2 - Select One
A rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
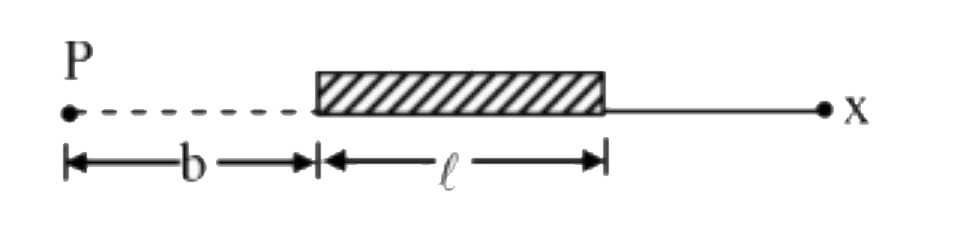 AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb) - Question 3 - Select One
A rod lies along the x-axis with one end at the origin and the other at x→∞. It carries a uniform charge λ C/m. The electric field at the point x = -a on the axis will be
A→E=λ4πε0a(−ˆi)B→E=λ4πε0a(ˆi)C→E=λ2πε0a(−ˆi)DE=λ2πε0a(ˆi)
A continuous line of charge oflength 3d lies along the x-axis, extending from x+d tox+4d . the line carries a uniform linear charge density λ.

In terms of d,λ and any necessary physical constants, find the magnitude of the electric field at the origin:View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View SolutionA rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?
 View Solution
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View Solution
