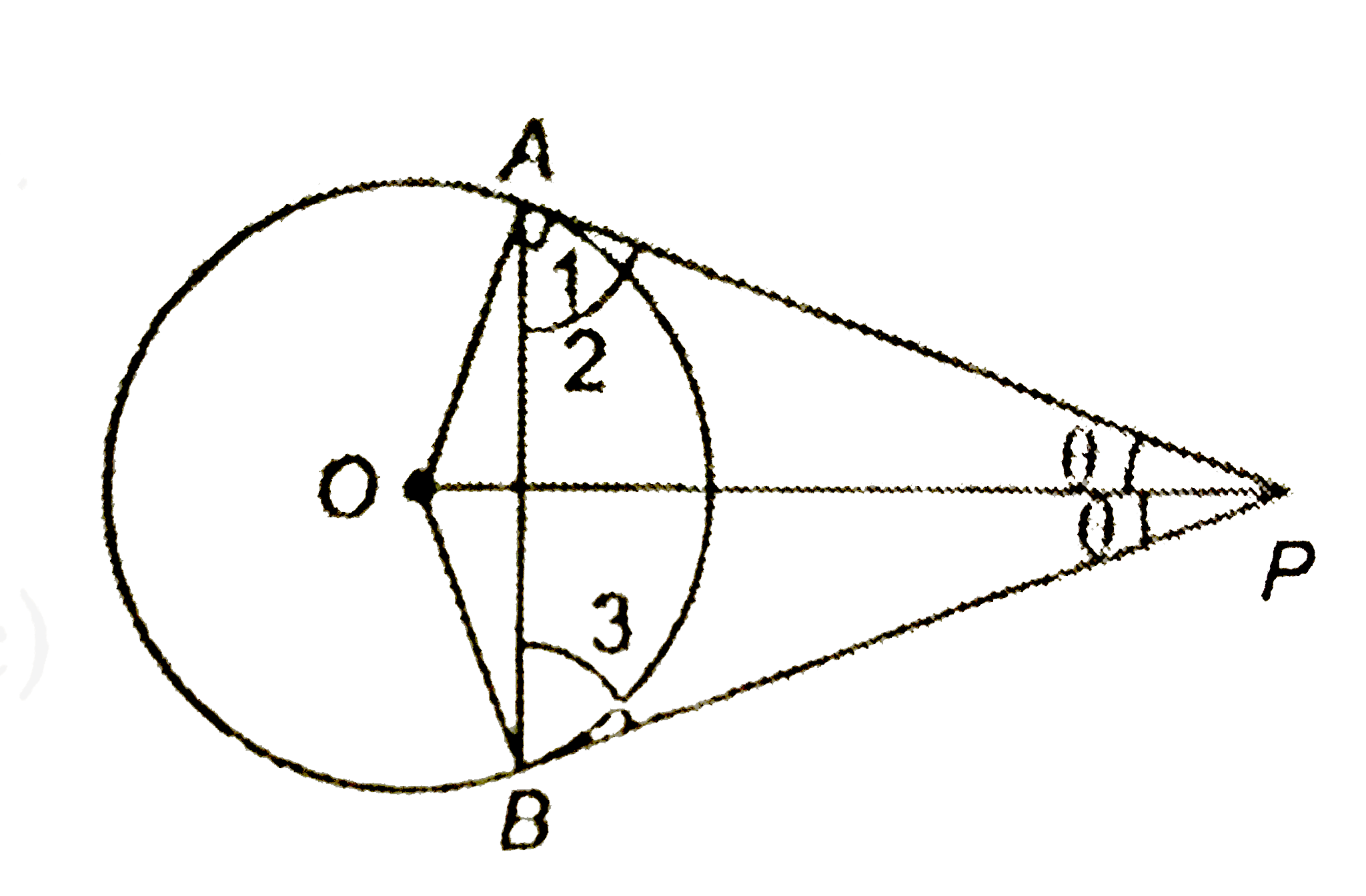
In a circle, OP is equal to diameter of the circle. PA and PB are two tangents. Prove that △ABP is an equilateral triangle.
The correct Answer is:60∘
Topper's Solved these Questions
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - ASSERTION AND REASON BASED QUESTIONS
2 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT
5 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - LONG ANSWER TYPE QUESTIONS
3 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Assertion and Reasoning Based Questions
2 Videos
Similar Questions
Knowledge Check
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
ARectangleBSquareCCyclicDNone of theseTwo circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘
In the given fig. OP is equal to the diameter of the circle with centre O. Prove that ΔABP is an equilateral triangle.
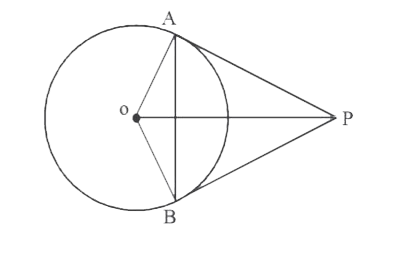
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.

View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.

View Solution