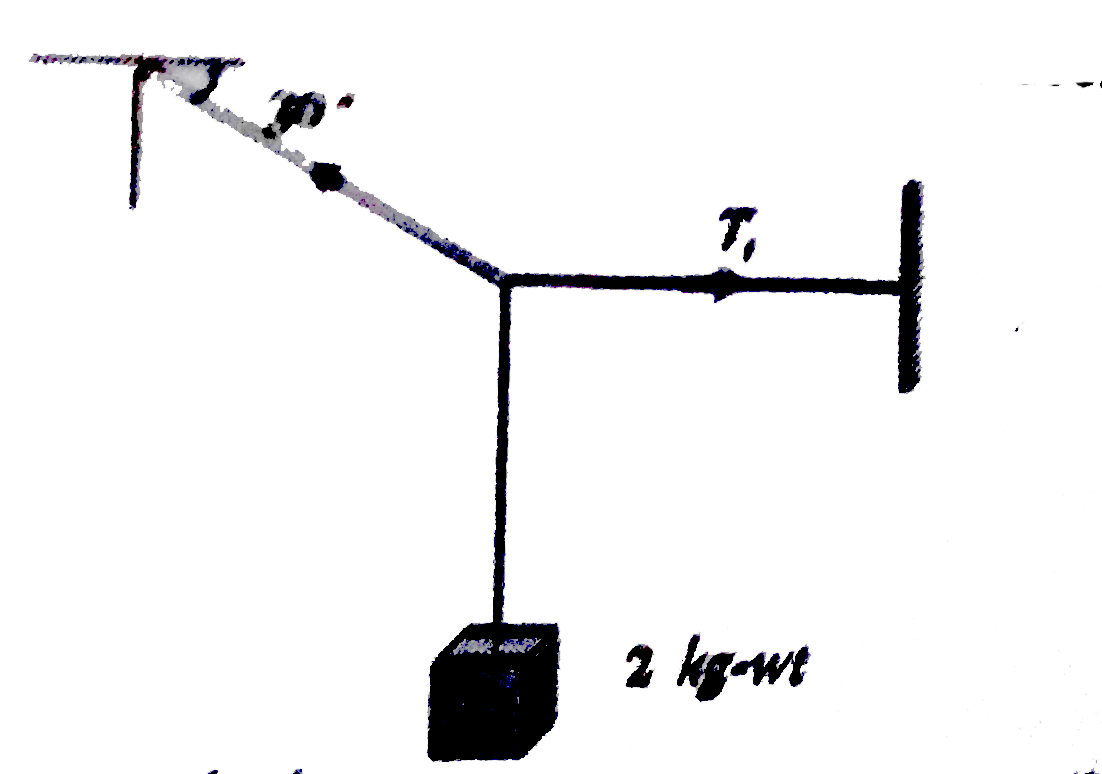
A body of weight 2 kg is suspended as shown in the figure. The tension $T_{1}$ in the horizontal string (in kg wt ) is

A

$2 / \sqrt{3}$

B

$\sqrt{3} / 2$

C

$2 \sqrt{3}$

D

2

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$T {cos 60}^{\circ} = 20$
$\Rightarrow T = 40 N$
$T {sin 60}^{\circ} = T_{1}$
$\Rightarrow T_{1} = 40 \times \frac{\sqrt{3}}{2} = 20 \sqrt{3}$
$\Rightarrow T_{1} = 2 \sqrt{3}$ kg wt

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass 10 kg is suspended by three strings as shown in figure . Tension $T_{2}$ is

A100N
B $\frac{100}{\sqrt{3}} N$
C $\sqrt{3} \times 100 N$
D $50 \sqrt{3} N$
Question 2 - Select One
Three equal weight $A, B$ and $C$ of mass $2 k g$ each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights $B$ and $C$ is approximately

Azero
B $13 N$
C $3.3 N$
D $19.6 N$
Question 3 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

A188 N
B2=368 N
C288 N
D168 N

ERRORLESS-NEWTON'S LAWS OF MOTION-NCERT BASED QUESTION (MOTION OF CONNECTED BODIES)

Home
Ask Doubt
Profile