Two blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
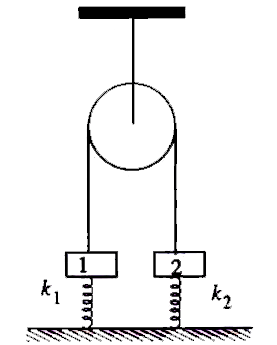
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–
Either (a1=a2=(k1+k2)2m)or(a1=k1Xm−g) and (a2=k3xm+g)
(a1=a2=(K1+k2)x2m) Only
(a1=a2=(k1−k2)x2m)Only
Either (a1=a2(K1−k2)2m)or(a1=a2(k1k2)(k1+k2)m−g)
The correct Answer is:B
When block 1 is slowly pulled down as distance x and released
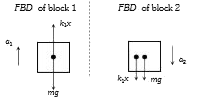
k1x−mg=ma1 …….(i)
⇒a1=k1xm−g
k2x+mg=ma2 ………..(ii)
if a1=a2, then add equation (i) + (ii)
2ma=k1x+k2x
⇒a=a1=a2=(k1+k2)x2m
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - PAST YEARS QUESTIONS14videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION (EQUILIBRIUM OF FORCES)4videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON19videos
MOTION IN TWO DIMENSION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason25videos
ROTATIONAL MOTION
Similar Questions
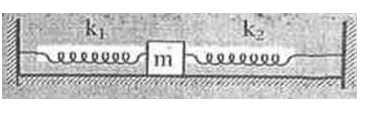
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 View Solution
View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32) - Question 2 - Select One
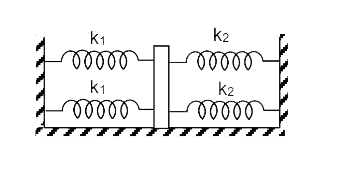
A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m - Question 3 - Select One or More
Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this process
The figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
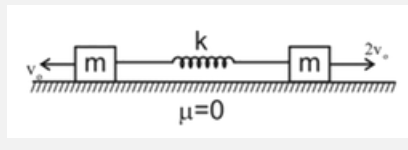 View Solution
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
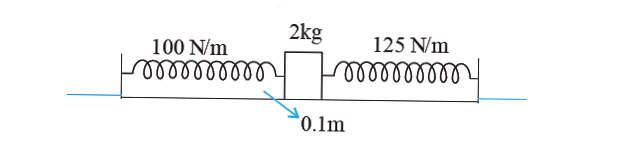
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
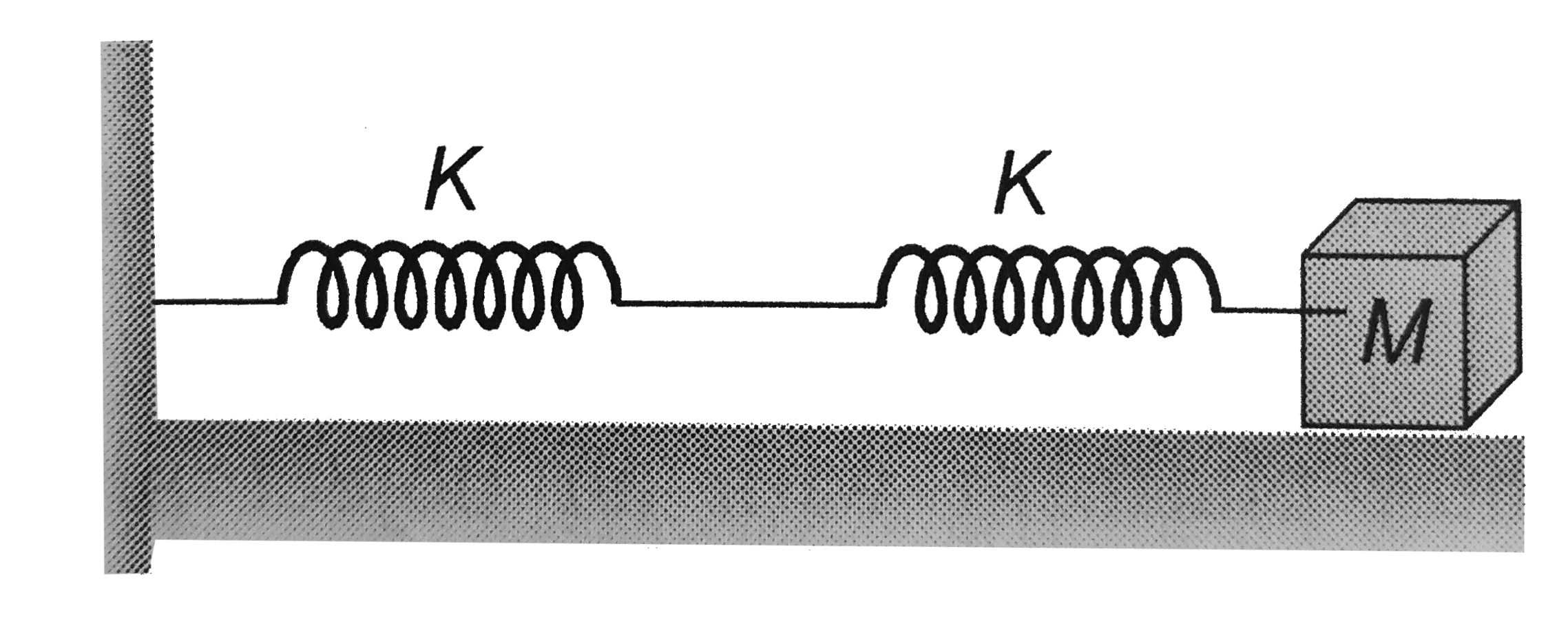 View Solution
View Solution

