In Fig. if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then
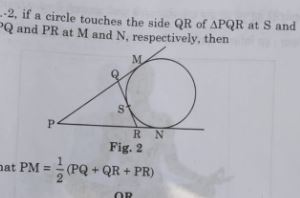
prove that PM=12(PQ+QR+PR)
Step by step video & image solution for In Fig. if a circle touches the side QR of DeltaPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = 1/2(PQ + QR + PR) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?
A160B320C120D96S and U are two points on the side PQ of ΔPQR , such that QU=PS . If ST||QR and UV∣∣PR , then
ATV||PQBTV⊥PQCTV and PQ intersect at 60∘DTV and PQ intersect at 45∘In a triangle PQR, P is the largest angle and cosP=1/3. Further the incircle of the triangle touches the sides PQ. QR and PR at N, L and M, respectively, such that the length of PN, QL, and RM are consecutive even integers. Then possible length (s) of the side(s) of the triangle is (are)
A16B18C24D22
M and N are the points on sides QR and PQ respectively of a △PQR, right angled at Q. prove that PM2+RN2=PR2+MN2
View Solution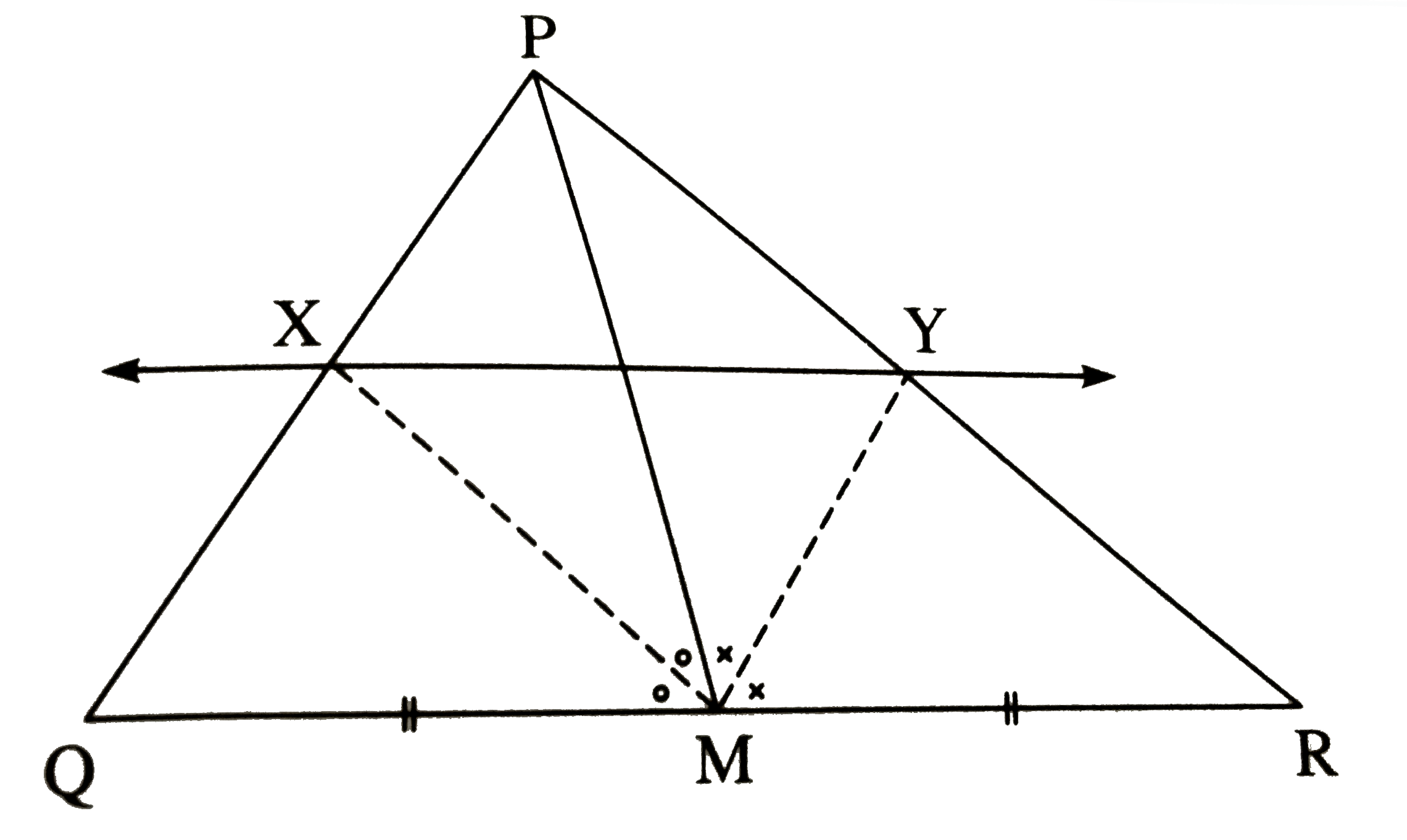
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY∣∣QR.
Complete the proof byfilling in the boxes:
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS.
View SolutionIn ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.
View SolutionPQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View Solution