M and N are the points on sides QR and PQ respectively of a △PQR, right angled at Q. prove that PM2+RN2=PR2+MN2
To prove that PM2+RN2=PR2+MN2 in triangle PQR where Q is the right angle, we will use the Pythagorean theorem.
1. Identify the Right Triangle:
- We have triangle PQR with Q as the right angle.
- Points M and N are located on sides QR and PQ respectively.
2. Apply the Pythagorean Theorem in Triangle PQM:
- In triangle PQM, we can apply the Pythagorean theorem:
PM2=PQ2+QM2(1)
3. Apply the Pythagorean Theorem in Triangle QRN:
- In triangle QRN, we again apply the Pythagorean theorem:
RN2=QR2+QN2(2)
4. Add Equations (1) and (2):
- Now, we add the two equations:
PM2+RN2=(PQ2+QM2)+(QR2+QN2)
5. Combine Terms:
- Rearranging gives us:
PM2+RN2=PQ2+QR2+QM2+QN2
6. Use the Pythagorean Theorem on Triangle PQR:
- Since PQR is a right triangle, we know:
PQ2+QR2=PR2(3)
7. Substitute Equation (3) into the Combined Equation:
- Substitute PQ2+QR2 from equation (3) into the previous equation:
PM2+RN2=PR2+QM2+QN2
8. Recognize QM2+QN2:
- Notice that QM2+QN2 represents the square of the length of segment MN (by the Pythagorean theorem in triangle QMN):
MN2=QM2+QN2(4)
9. Final Substitution:
- Substitute equation (4) into the equation:
PM2+RN2=PR2+MN2
10. Conclusion:
- Thus, we have proved that:
PM2+RN2=PR2+MN2
- We have triangle PQR with Q as the right angle.
- Points M and N are located on sides QR and PQ respectively.
- In triangle PQM, we can apply the Pythagorean theorem:
PM2=PQ2+QM2(1)
- In triangle QRN, we again apply the Pythagorean theorem:
RN2=QR2+QN2(2)
- Now, we add the two equations:
PM2+RN2=(PQ2+QM2)+(QR2+QN2)
- Rearranging gives us:
PM2+RN2=PQ2+QR2+QM2+QN2
- Since PQR is a right triangle, we know:
PQ2+QR2=PR2(3)
- Substitute PQ2+QR2 from equation (3) into the previous equation:
PM2+RN2=PR2+QM2+QN2
- Notice that QM2+QN2 represents the square of the length of segment MN (by the Pythagorean theorem in triangle QMN):
MN2=QM2+QN2(4)
- Substitute equation (4) into the equation:
PM2+RN2=PR2+MN2
- Thus, we have proved that:
PM2+RN2=PR2+MN2
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions9videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Short Questions10videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6c11videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
P and Q are points on the sides CA and CB respectively of ABC, right-angled at C. Prove that AQ2+BP2=AB2+PQ2.
View SolutionIn a right triangle ABC , right angled at C, P and Q are the points of the sides CA and CB respectively , which divide these sides in the ratio 2:1 Prove that
9(AQ2+BP2)=13AB2View Solution
Knowledge Check
- Question 1 - Select One
P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
ABC2+PQ2BAB2+PC2CAB2+PQ2DBC2+AC2 - Question 2 - Select One
PQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
A32B52C2DNone of these
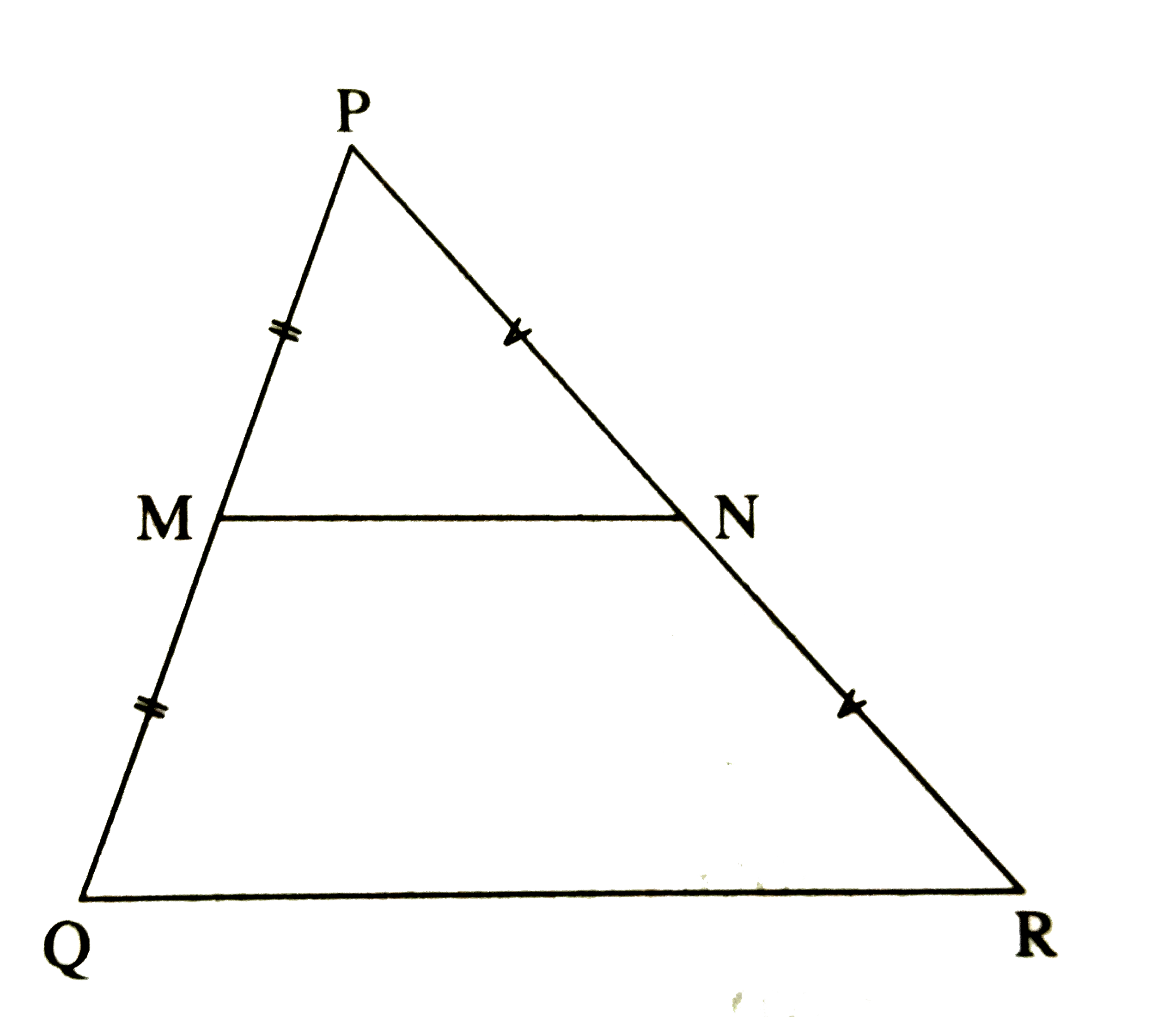
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .View SolutionIn A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
 View Solution
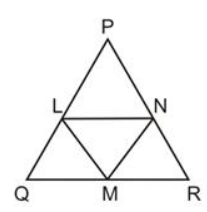
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
 View Solution
View SolutionE and F are points on the sides PQ and PR respectively of a ΔPQR. Show that Ef||QR. If PQ = 1.28 cm,PR= 2.56 cm,PE = 0.18 cm and PF= 0.36 cm.
View SolutionPQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View Solution

