In Figure, the angles of elevation of the top of a tower AB of height 'h'm, from two points P and Q at a distance of x m and y m from the base of the tower respectively and in the same straight line with it, are $60^{\circ} and 30^{\circ}$ , respectively. Prove that $h^{2} = x y$ .

Video Solution

Answer

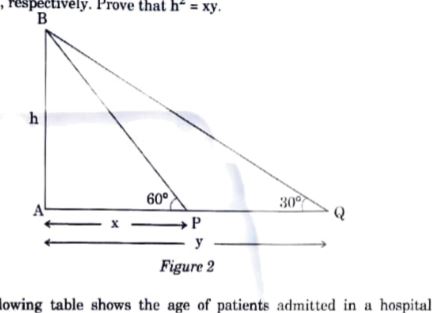
Step by step video & image solution for In Figure, the angles of elevation of the top of a tower AB of height 'h'm, from two points P and Q at a distance of x m and y m from the base of the tower respectively and in the same straight line with it, are 60^@ and 30^@, respectively. Prove that h^2 = xy. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is
A5m
B15m
C $5 \sqrt{2}$ m
D $75 m$
Question 2 - Select One
The angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A $\sqrt{a b}$
B $\frac{a}{b}$
Cab
D $a^{2} b^{2}$
Question 3 - Select One
If the angles of elevation of the top of a tower from two places situated at distances 21 m and x m from the base of the tower are $45^{\circ} and 60^{\circ}$ respectively, then what is the value of x?
A $7 \sqrt{3} m$
B $7 - \sqrt{3} m$
C $7 + \sqrt{3} m$
D $14$

X BOARDS-QUESTION PAPER 2022 TERM 2 SET 2 STANDARD-SECTION B

Home
Ask Doubt
Profile

In Figure, the angles of elevation of the top of a tower AB of height 'h'm, from two points P and Q at a distance of x m and y m from the base of the tower respectively and in the same straight line with it, are 60 ∘ and 30 ∘ , respectively. Prove that h 2 = x y .

Topper's Solved these Questions

Similar Questions

Knowledge Check

The angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is

The angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is

If the angles of elevation of the top of a tower from two places situated at distances 21 m and x m from the base of the tower are 45∘and60∘ respectively, then what is the value of x?

X BOARDS-QUESTION PAPER 2022 TERM 2 SET 2 STANDARD-SECTION B

In Figure, the angles of elevation of the top of a tower AB of height 'h'm, from two points P and Q at a distance of x m and y m from the base of the tower respectively and in the same straight line with it, are $60^{\circ} and 30^{\circ}$ , respectively. Prove that $h^{2} = x y$ .

If the angles of elevation of the top of a tower from two places situated at distances 21 m and x m from the base of the tower are $45^{\circ} and 60^{\circ}$ respectively, then what is the value of x?