EMF of a cell is related to standard EMF, by the equation
Where k is reaction quotient and n the volume of electrons which is correct graphical representation
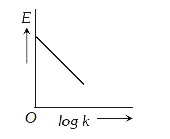
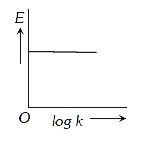
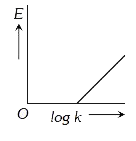
The correct Answer is:B
To solve the problem, we need to analyze the equation given and understand how to represent it graphically. The equation provided is:
E=E∘−0.0591nlogK
Where:
- E is the EMF of the cell.
- E∘ is the standard EMF.
- n is the number of electrons transferred in the reaction.
- K is the reaction quotient.
1. Identify the Variables:
- From the equation, we can identify that E (EMF of the cell) is dependent on logK (the logarithm of the reaction quotient).
2. Rearranging the Equation:
- The equation can be rearranged to fit the linear equation format Y=C−MX:
E=E∘−(0.0591n)logK
- Here, we can identify:
- Y (dependent variable) = E (EMF of the cell)
- C (intercept) = E∘ (standard EMF)
- M (slope) = −0.0591n
- X (independent variable) = logK
3. Determine the Slope:
- The slope M is negative since it is represented as −0.0591n. This indicates that as logK increases, E decreases.
4. Graphical Representation:
- On a graph, the Y-axis will represent the EMF of the cell (E), and the X-axis will represent logK.
- The graph will have a negative slope, indicating that as the reaction quotient K increases, the EMF of the cell decreases.
5. Finding the Correct Option:
- We need to identify the option that shows a negative slope. Based on the analysis:
- Option A: Positive slope
- Option B: Negative slope (correct option)
- Option C: Zero slope
- Option D: Positive slope
- Therefore, the correct option is Option B.
- E is the EMF of the cell.
- E∘ is the standard EMF.
- n is the number of electrons transferred in the reaction.
- K is the reaction quotient.
- From the equation, we can identify that E (EMF of the cell) is dependent on logK (the logarithm of the reaction quotient).
- The equation can be rearranged to fit the linear equation format Y=C−MX:
E=E∘−(0.0591n)logK
- Here, we can identify:
- Y (dependent variable) = E (EMF of the cell)
- C (intercept) = E∘ (standard EMF)
- M (slope) = −0.0591n
- X (independent variable) = logK
- The slope M is negative since it is represented as −0.0591n. This indicates that as logK increases, E decreases.
- On a graph, the Y-axis will represent the EMF of the cell (E), and the X-axis will represent logK.
- The graph will have a negative slope, indicating that as the reaction quotient K increases, the EMF of the cell decreases.
- We need to identify the option that shows a negative slope. Based on the analysis:
- Option A: Positive slope
- Option B: Negative slope (correct option)
- Option C: Zero slope
- Option D: Positive slope
- Therefore, the correct option is Option B.
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - PAST YEARS QUESTIONS51videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - Assertion & Reason6videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT BASED QUESTIONS (Photochemical Reaction)4videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CARBOXYLIC ACIDSEXERCISE - Assertion & Reason5videos
CARBOXYLIC ACIDS
- BOOK - ERRORLESSCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - Assertion & Reason4videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The standard electrode potentials at 298 K are given below:
E0Zn2+∣Zn = -0.76 volt and ,E0Fe2+∣Fe = -0.44 volt ,E0H2+∣H2 = -0.0volt
Which of the two electrodes should be combined to form a cell having highest EMF? Identify the cathode and the anode and write the cell reaction. Also mention the direction of flow of electrons in the external as well as the internal circuit.View SolutionThe standard electrode potentials at 298 K are given below:
E0Zn2+∣Zn = -0.76 volt and ,E0Fe2+∣Fe = -0.44 volt ,E0H2+∣H2 = -0.0volt
Which of the two electrodes should be combined to form a cell having highest EMF? Identify the cathode and the anode and write the cell reaction. Also mention the direction of flow of electrons in the external as well as the internal circuit.View Solution
Knowledge Check
- Question 1 - Select One
Assertion: The emf of a cell is related with equilibrium constant of the cell reaction as Ecell=0.0591nlog K.
Reason: As Ecell changes with concentration of the electrodes, K of cell reaction also changes with concentration.AIf both assertion and reason are true, and reason is the true explanation of the assertionBif both assertion and reason are true, but reason is not the true explanation of the assertion.Cif assertion is true, but reason is false.DIf both assertion and reason are false. - Question 2 - Select One
The cell potential (Ecell) of a reaction is related as △G=−nFEcell, where △G represents max. useful electrical work
n=no. of moles of electrons exchanged during the section
for reversible cell reaction d(△G)=(△rV)dp−(△rS),dT
at constant pressure d(△G)=−(△rS).dT
:' At constant pressure △G=△H−T.△S
:. /_\G=/+\H+T(d(/_\G))/((dT)_P)<br>((dE_(cell))/(dT))_Pisknownastemperturecoefficientofthee.m.fofthecell.<br>Thetemperaturecoefficientofthee.m.fofcell,((dE)/(dT))_P si given by:AnF△SB△SnFC△SnFTD#REF! - Question 3 - Select One
In an electrochemical cell, if E∘ is the e.m.f. of the cell involving 'n' mole of electrons, then ΔG∘ is
AΔG∘=nFE∘BΔG∘=−nFE∘CE∘=nFΔE∘DΔG=nF/E∘
A group of N cells whose emf varies directly with the internal resistance as per the equation EN=1.5rN are connected as shown in the figure. The current in the circuit is
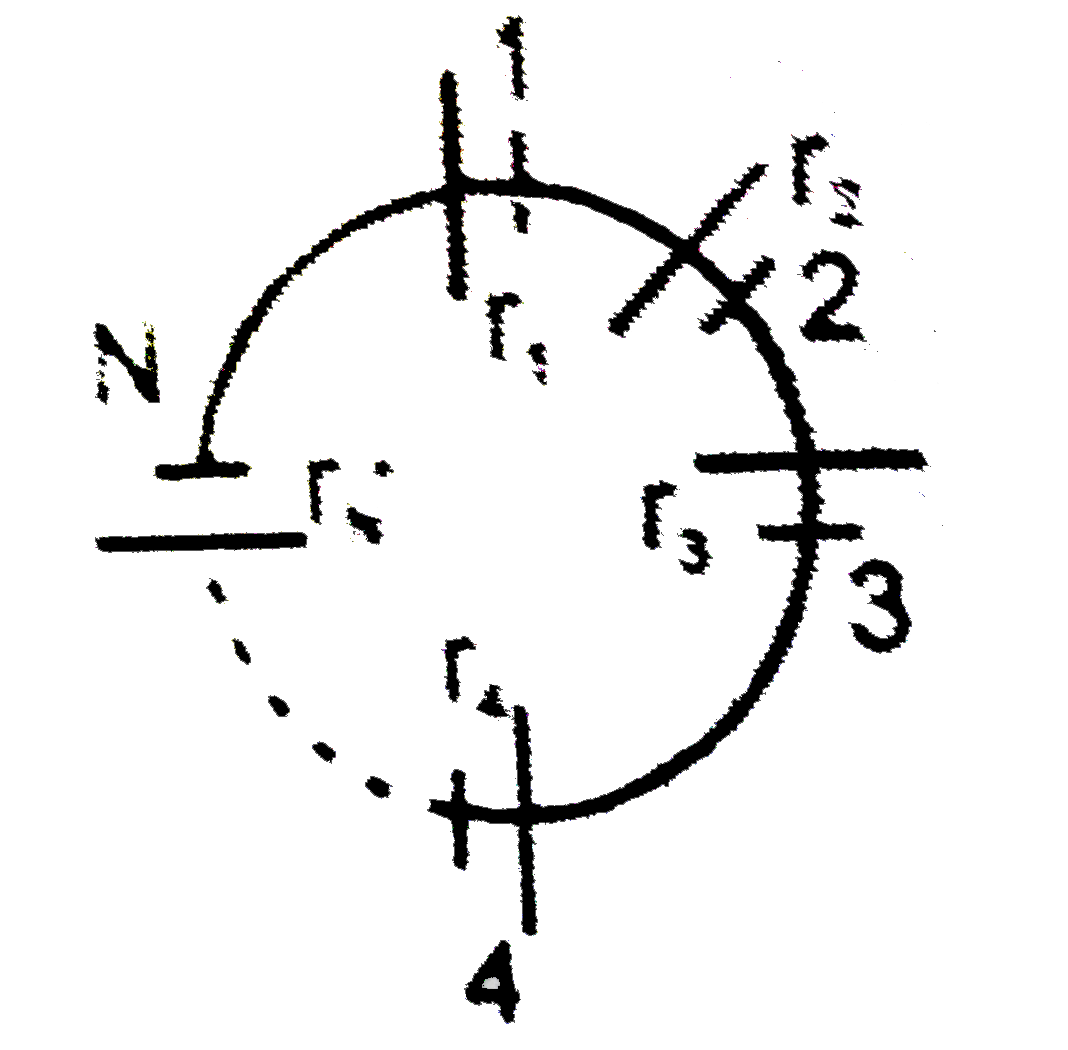View Solution
A group of N cells where e.m.f. varies directly with the internal resistance as per the equation EN=1.5rN are connected as shown in the figure. The current I in the circuit is:View SolutionThe driving force ΔG diminishes to zero on the way to equilibrium, just as in any other spontaneous process. Both ΔG and the corresponding cell potential (E=−ΔGnF) are zero when the redox reaction comes to equilibrium. The Nernst equation for the redox process of the cell may be given as :
E=E∘−0.059nlogQ
The key to the relationship is the standard cell potential E∘, derived from the standard free energy changes as :
E∘=−ΔG∘nF
At equilibrium, the Nernst equation is given as :
E∘=0.059nlogK
The equilibrium constant Kc for the reaction :
Cu(s)+2Ag+(aq.)+2Ag(s) (E∘cell=0.46V) will be :View SolutionThe driving force ΔG diminishes to zero on the way to equilibrium, just as in any other spontaneous process. Both ΔG and the corresponding cell potential (E=−ΔGnF) are zero when the redox reaction comes to equilibrium. The Nernst equation for the redox process of the cell may be given as :
E=E∘−0.059nlogQ
The key to the relationship is the standard cell potential E∘, derived from the standard free energy changes as :
E∘=−ΔG∘nF
At equilibrium, the Nernst equation is given as :
E∘=0.059nlogK
The nature of graph of E∘cell against logKc is a/an :View SolutionThe driving force ΔG diminishes to zero on the way to equilibrium, just as in any other spontaneous process. Both ΔG and the corresponding cell potential (E=−ΔGnF) are zero when the redox reaction comes to equilibrium. The Nernst equation for the redox process of the cell may be given as :
E=E∘−0.059nlogQ
The key to the relationship is the standard cell potential E∘, derived from the standard free energy changes as :
E∘=−ΔG∘nF
At equilibrium, the Nernst equation is given as :
E∘=0.059nlogK
the equilibrium constant Kc will be equal to Q, when :View Solution