Rate constant k varies with temperature T(k) as given by equation
logk=logA−Ea2.303RT
A plot between log k and 1T is straight line from the graph we can say
Ea=2.303R×slope
Ea=2.303R2×tanθ
Ea=Rtanθ
None of these
The correct Answer is:A
To solve the question regarding the relationship between the rate constant k and temperature T as given by the equation:
logk=logA−Ea2.303RT
we can follow these steps:
Step 1: Identify the equation form
The equation resembles the linear form y=mx+c, where:
- y is logk
- m is the slope of the line, which is −Ea2.303R
- x is 1T
- c is logA
Step 2: Understand the slope
From the equation, we can see that the slope of the line plotted between logk and 1T is equal to −Ea2.303R. This indicates that the slope is negative, which implies that as the temperature increases (and thus 1T decreases), the value of logk increases.
Step 3: Relate slope to activation energy
Since the slope is related to the activation energy Ea, we can express the activation energy as:
Ea=−slope×2.303R
Step 4: Conclusion
From the graph, we can conclude that the activation energy Ea can be determined from the slope of the line. The negative slope indicates that the activation energy is a positive quantity, which is consistent with the physical interpretation of activation energy in chemical kinetics.
Final Answer
Thus, from the graph, we can say that the activation energy Ea can be calculated using the slope of the line obtained from the plot of logk versus 1T.
---
The equation resembles the linear form y=mx+c, where:
- y is logk
- m is the slope of the line, which is −Ea2.303R
- x is 1T
- c is logA
From the equation, we can see that the slope of the line plotted between logk and 1T is equal to −Ea2.303R. This indicates that the slope is negative, which implies that as the temperature increases (and thus 1T decreases), the value of logk increases.
Since the slope is related to the activation energy Ea, we can express the activation energy as:
Ea=−slope×2.303R
From the graph, we can conclude that the activation energy Ea can be determined from the slope of the line. The negative slope indicates that the activation energy is a positive quantity, which is consistent with the physical interpretation of activation energy in chemical kinetics.
Thus, from the graph, we can say that the activation energy Ea can be calculated using the slope of the line obtained from the plot of logk versus 1T.
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - PAST YEARS QUESTIONS51videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - Assertion & Reason6videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT BASED QUESTIONS (Photochemical Reaction)4videos
CHEMICAL KINETICS
- BOOK - ERRORLESSCHAPTER - CARBOXYLIC ACIDSEXERCISE - Assertion & Reason5videos
CARBOXYLIC ACIDS
- BOOK - ERRORLESSCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - Assertion & Reason4videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
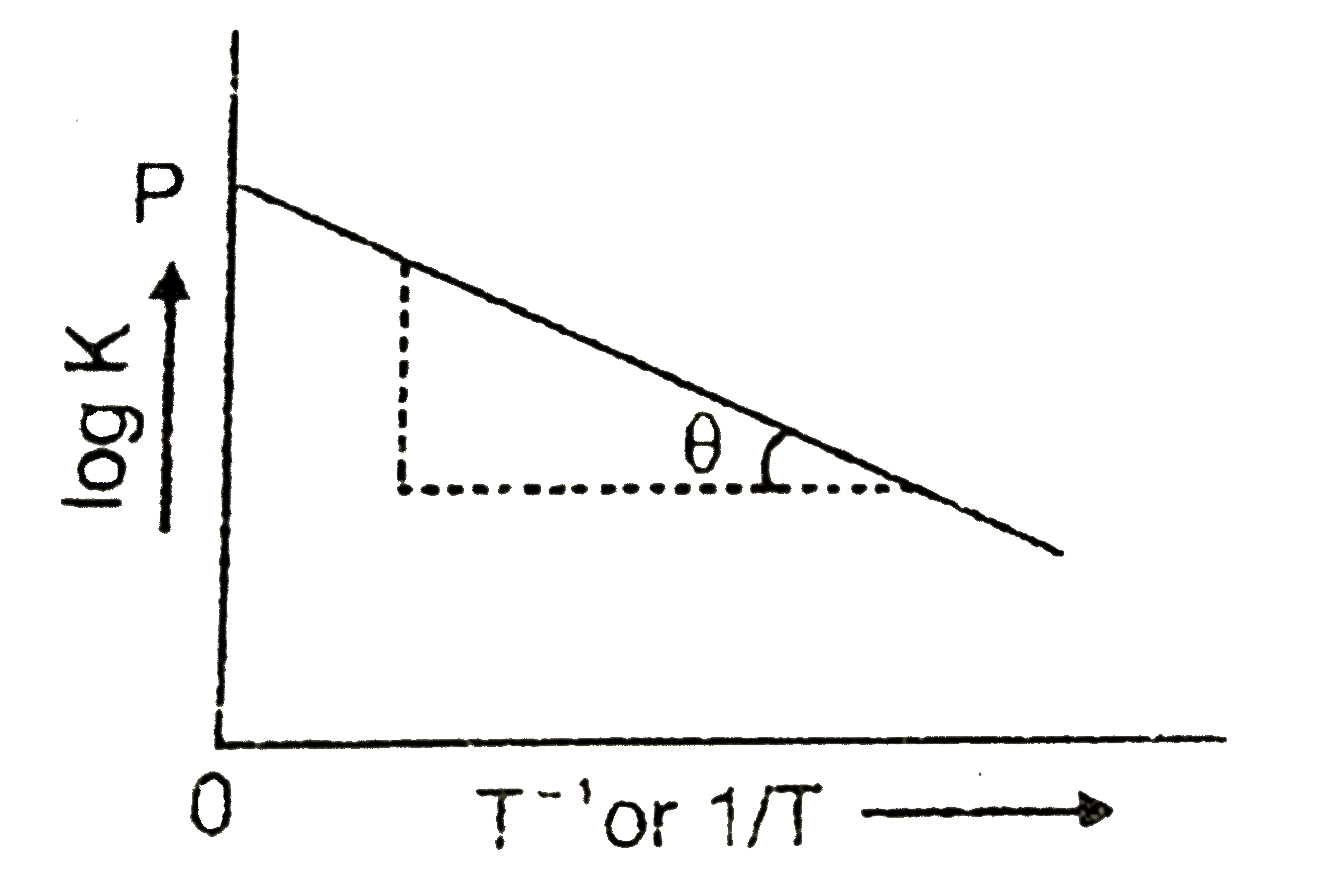
Variation of equiibrium constant K with temperature T is given by van 't Holf equation,
logK=logA−ΔH∘2.303RT
A graph between log K and T−1 was a straight line as shown in the figure and having θ=tan−1(0.5)andOP=10. Calculate:
(a) ΔH∘ (standard heat of reaction)when T=300K,
(b) A (pre-exponetial factor),
(c) Equilibrium constant K at 300K,
(d) Kat900KifΔH∘ is independent of temperature.
 View Solution
View SolutionThe graph between logk versus 1/T is a straight line.
View Solution
Knowledge Check
- Question 1 - Select One or More
Rate constant k varies with temperature by equation, log k (min+−1)=5−2000T(K) We can conclud:
Apre-exponential factor A is 5BEa is 2000 kcalCpre-exponential factor A is 105DEa is 9.212 kcal - Question 2 - Select One
Rate constant k of a reaction varies with temperature according to the equation, log k = constant -Ea2.303RT When a graph is plotted for logk versus 1/T a straight line with a slope -5632 is obtained. The energy of activation for this reaction is
A127.67 kJ mol−1B107.84 kJ mol−1C86 kJ mol−1D246.8 kJ mol−1 - Question 3 - Select One or More
Rate constant k varies with temperature by equation logk(−1min)=log5−2000kcalRT×2.303. We can conclude that
AThe pre-exponential factor A is 105.BEa is 2000kcalCEa is 9.12kcalDThe pre-exponential factor A is 5
Rate constant 'k' of a reaction varies with temperature 'T' according to the equation:
logk=logA−Ea2.303R(1T)
where Ea is the activation energy. When a graph is plotted for log k vs 1T, a straight line with a slope of -4250 K is obtained. Calculate 'Ea' for the reaction. [R=8.314JK−1mol−1]View SolutionThe rate constant 'k'. For a reaction varies with temperature 'T' according to the question. logk=logA−Ea2.303R(1T)
Where Ea is the activation energy. When a graph is plotted for logkvs1/T, a straight line with a slope of −4250 K is obtained. Calcualte Ea for this reaction.View SolutionThe rate constant 'k'. For a reaction varies with temperature 'T' according to the question. logk=logA−Ea2.303R(1T)
Where Ea is the activation energy. When a graph is plotted for logkvs1/T, a straight line with a slope of −4250 K is obtained. Calcualte Ea for this reaction.View Solution(a) For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
(b) Rate constant 'K' of a reaction varies with temperature 'T' according to the equation : logK=logA−Ea2.303R(1T)
Where Ea is the activation energy. When a graph is plotted for log k Vs 1T a straight line with a slope of -4250 K is obtained. Calculate Ea for the reaction.
(R=8.314JK−1mol−1)View SolutionA graph plotted between log k vs 1T is represented by
View Solution

