The volume of the solid obtained by revolving the curve about x - axis between the lines x = 0 and x = 2 is
To find the volume of the solid obtained by revolving the curve y=x3 about the x-axis between the lines x=0 and x=2, we can use the disk method. The volume V is given by the integral:
V=π∫ba(f(x))2dx
where f(x) is the function being revolved, and (a,b) are the bounds of integration.
1. Identify the function and the bounds:
- The function is f(x)=x3.
- The bounds are a=0 and b=2.
2. Set up the integral for the volume:
- The volume V can be expressed as:
V=π∫20(x3)2dx
3. Simplify the integrand:
- Calculate (x3)2:
(x3)2=x6
- Thus, the integral becomes:
V=π∫20x6dx
4. Compute the integral:
- The integral of x6 is:
∫x6dx=x77
- Now evaluate it from 0 to 2:
V=π(x77)20=π(277−077)=π(1287−0)=128π7
5. Final result:
- The volume of the solid obtained by revolving the curve y=x3 about the x-axis between x=0 and x=2 is:
V=128π7
- The function is f(x)=x3.
- The bounds are a=0 and b=2.
- The volume V can be expressed as:
V=π∫20(x3)2dx
- Calculate (x3)2:
(x3)2=x6
- Thus, the integral becomes:
V=π∫20x6dx
- The integral of x6 is:
∫x6dx=x77
- Now evaluate it from 0 to 2:
V=π(x77)20=π(277−077)=π(1287−0)=128π7
- The volume of the solid obtained by revolving the curve y=x3 about the x-axis between x=0 and x=2 is:
V=128π7
Topper's Solved these Questions
Similar Questions
Knowledge Check
The volume of the solid obtained by revolving about y-axis the area enclosed between the ellipse x2+9y2=9 and the strangth line x+3y=3, in the first quadrant is
A3πB4πC6πD9πThe volume of the solid generated by the revolution of the curve y=a3a2+x2 about x-axis is :
A12π3a2Bπ3a2C12π2a3Dπ2a3The volume of the solid generated by the revolution of the curve y=a3a2+x2 about x-axis is :
A12π3a2Bπ3a2C12π2a3Dπ2a3
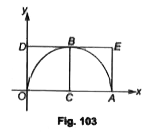
Given: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View SolutionFind the area of the region bounded by the curve y=x2 , the x-axis, and the lines x = 1 and x = 3.
View SolutionThe area between the curve y=x2,x-axis and the lines x=0andx=2 is :
View SolutionArea bounded by the curve y=ex, the X-axis and the lines x = 0, x = 2 is
View SolutionThe area bounded by the curve y=(x2+2)2+2x, X-axis and the lines x = 0, x = 2 is
View Solution
