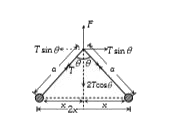
Two particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that, each mass is at a distance 'a' from the center P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is :

F2ma√a2−x2
F2mx√a2−x2
F2m.xa
F2m√a2−x2x
The correct Answer is:B
F=2Tcosθ⇒T=F2cosθ
Magnitude of acceleration of the particle.
a=Tsinθm=Ftanθ2m
=F2mx√a2−x2
Similar Questions
Two particles of mass m each are tied at the ends of a light string of length 2a . The whole system is kept on a frictionless horizontal surface with the string held tight so that, each mass is at a distance 'a' from the center P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x , is :
View SolutionTwo particles of mass 'm' each are tied at eh ends of a light string of length '2a' The whole system is kept on frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the centre P (as shown in figure). Now the mid point of the string is pulled vertically upwards with a small but constant force F As a result, the particles move towards each other on the surface the magnitude of acceleration, when the separation between them becomes 2x is:
View Solutionदो कण जिनमें से प्रत्येक का द्रव्यमान m है 2a लम्बाई की एक हल्की डोरी के किनारों पर बंधे है। यह सम्पूर्ण निकाय एक घर्षणहीन क्षैतिज तल पर इस प्रकार रखा है की डोरी तनी हुई है तथा प्रत्येक कण डोरी के मध्य-बिंदु P से 'a ' दुरी पर है (जैसे की चित्र में दिखाया गया है)। अब डोरी के मध्य- बिंदु को ऊर्ध्वाधर दिशा में ऊपर की ओर एक लघु, किन्तु एकसमान परिमाण के बल F से खिंचा जाता है। परिणाम स्वरूप, कण क्षैतिज तल पर एक-दूसरे की ओर चलने लगते है। जब कणों के बीच दुरी 2x हो जाती है, तब उनके त्वरणों का परिणाम है:

View SolutionAs shown in the figure, two particle each of mass m tied at the ends of a light string of length 2a are kept on a frictionless horizontal surface. When the mid-point (P) of the string is pulled vertically upwards with a small but constant force F, the particles move towards each other on the surface. Magnitude of acceleration of each particle, when the separation between them becomes 2x is
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance 'a' from the center P (as shown in figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is :
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
View SolutionTwo identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.

View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View Solution
