In figure TQ, TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=75∘,∠PRT=25∘,then determine the values of ∠TQR and ∠QTR.
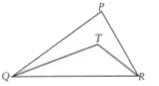
27.5∘,127.5∘
127.5∘,27.5∘
137.5∘,37.5∘
None of these
The correct Answer is:A
Topper's Solved these Questions
- LINES AND ANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -2 MATCH THE FOLLOWING)
2 Videos
- LINES AND ANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -2 ASSERTION & REASON TYPE)
5 Videos
- LINES AND ANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL -1)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - OLYMPIAD/HOTS CORNER
5 Videos
- NUMBER SYSTEMSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - NUMBER SYSTEMSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
In triangle PQR, the internal bisector of ∠Q and ∠R meets at 0. If ∠QPR=70∘, then what is the value (in degrees) of ∠QOR?
A45B125C115D110In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100
In Figure, PQ>PR.QS and RS are the bisectors of LQ and ∠R respectively. Prove that SQ>SR.
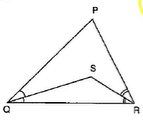
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn the given figure, the bisectors of ∠P and ∠Q meet at a point A.If ∠R=110∘ and ∠S=50∘, find measure of ∠PAQ
View SolutionIn Figure PS is the bisector of ∠QPR and PT ⊥QR . Show that ∠TPS=12(∠Q−∠R)
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.

View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.

View Solution
