In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that . 
Text Solution
The correct Answer is:.
|
Topper's Solved these Questions
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:NCERT Section (Exercise 10.1 (Fill in the blanks.))
Explore 10 Videos
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:NCERT Section (Exercise 10.2)
Explore 16 Videos
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:Olympiad/HOTS Corner
Explore 30 Videos
- ARITHMETIC PROGRESSIONS Book:MTG IIT JEE FOUNDATIONChapter:ARITHMETIC PROGRESSIONS Exercise:OLYMPIAD/HOTS CORNER
Explore 15 Videos
- CO-ORDINATE GEOMETRYBook:MTG IIT JEE FOUNDATIONChapter:CO-ORDINATE GEOMETRYExercise:Olympiad/HOTS Corner
Explore 40 Videos
Similar Questions
Knowledge Check
In the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD
 A90∘B80∘C45∘D60∘
A90∘B80∘C45∘D60∘In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
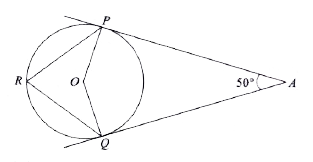 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
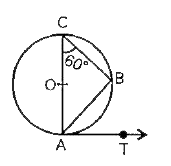 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘
In the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
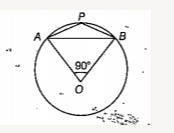
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
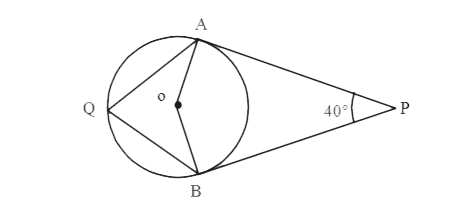
View SolutionIn Fig, O is the center of the circle. Find the angle of △ABC.

View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
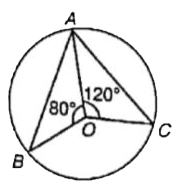
View SolutionIn the given figure O is the centre of the circle and ∠BAC=25∘, then the value of ∠ADB is :

View Solution
