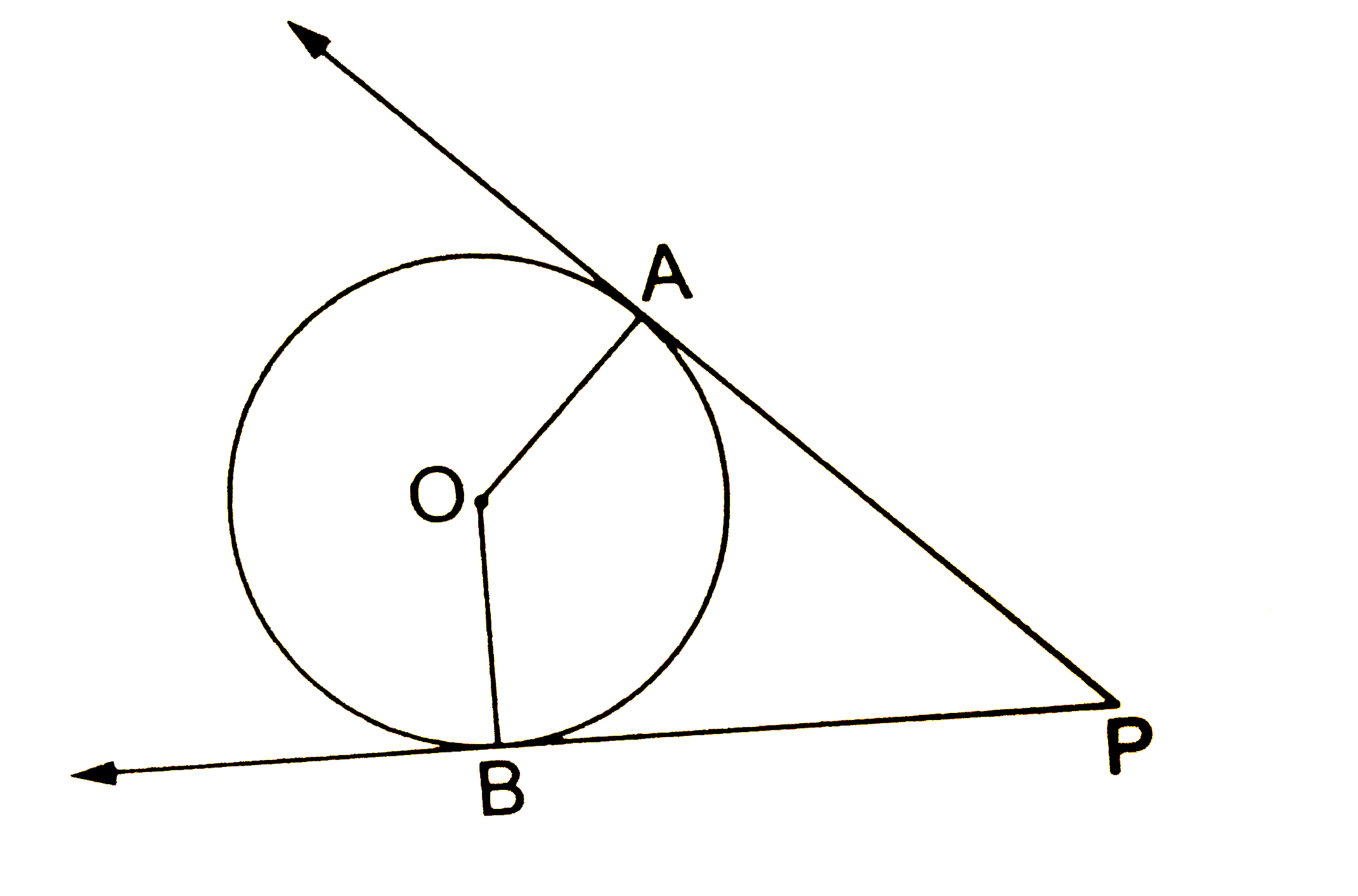
In the figure, O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic. 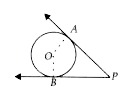
The correct Answer is:180∘
Topper's Solved these Questions
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:NCERT Section (Exercise 10.1 (Fill in the blanks.))
Explore 10 Videos
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:NCERT Section (Exercise 10.2)
Explore 16 Videos
- CIRCLESBook:MTG IIT JEE FOUNDATIONChapter:CIRCLESExercise:Olympiad/HOTS Corner
Explore 30 Videos
- ARITHMETIC PROGRESSIONS Book:MTG IIT JEE FOUNDATIONChapter:ARITHMETIC PROGRESSIONS Exercise:OLYMPIAD/HOTS CORNER
Explore 15 Videos
- CO-ORDINATE GEOMETRYBook:MTG IIT JEE FOUNDATIONChapter:CO-ORDINATE GEOMETRYExercise:Olympiad/HOTS Corner
Explore 40 Videos
Similar Questions
Knowledge Check
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
ARectangleBSquareCCyclicDNone of these
PA and PB are tangents to the circle and O is the centre of the circle . The radius is 5 cm and PO is 13 cm . Find the area PBOAAa) √1213Bb) 2413Cc) √2413Dd) 60
PA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View SolutionIf PAB are secant to the circle and PT is tangent segment; then PA×PB=PT2
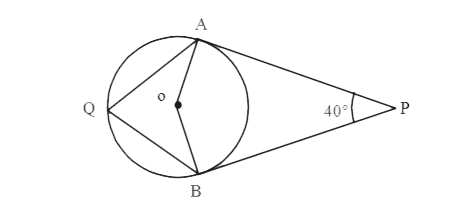
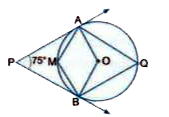
View SolutionIf Fig. 'O' is the centre of the circle Determine ∠AQBand∠AMB if PA and PB are tangents and ∠APB=75∘.
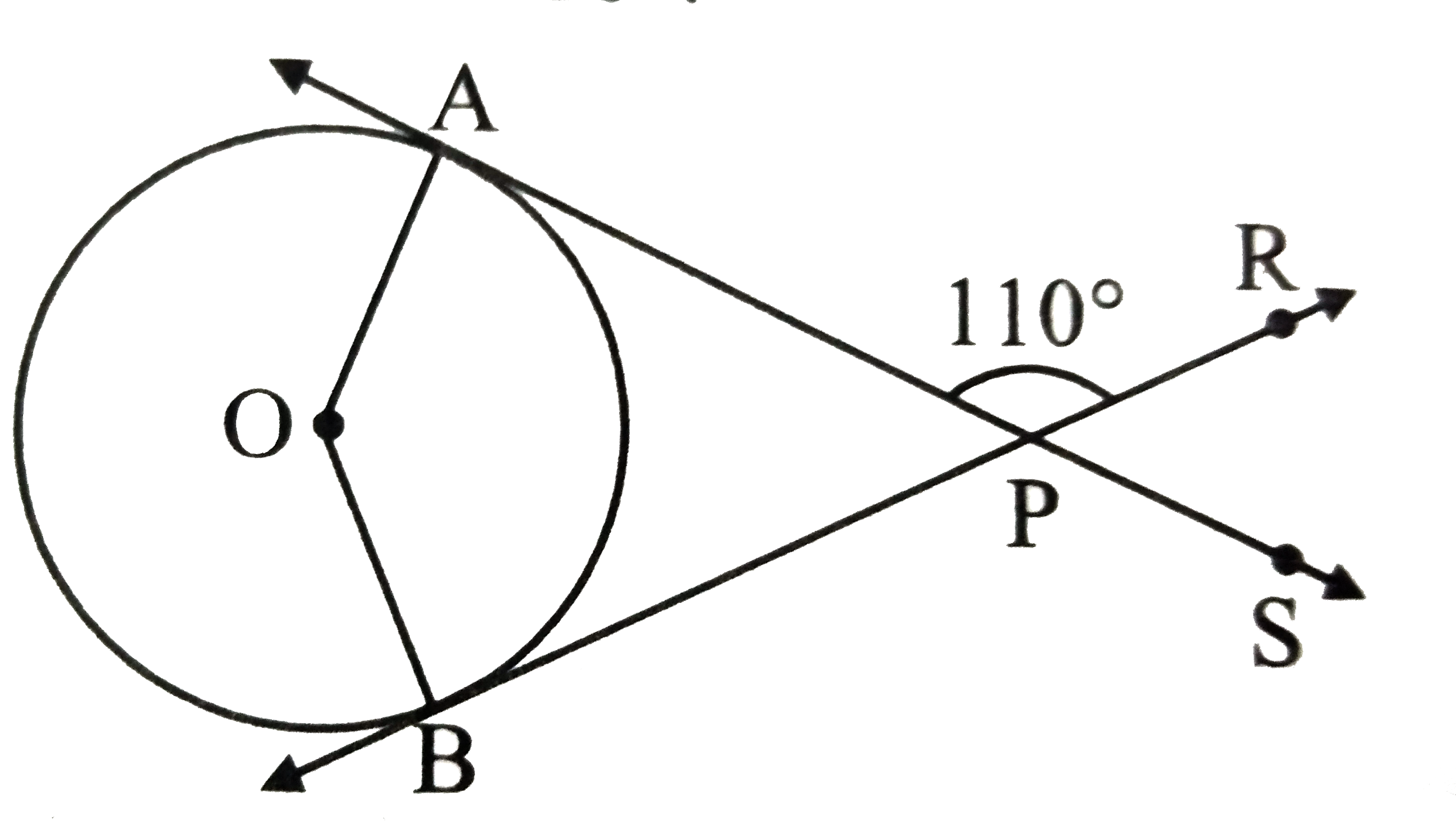
View SolutionFind the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR=110∘
View SolutionAs shown in the figure, PA is a tangent to a circle and PBC is a secant, so that PB = AB. Prove that PB.PC=AC2
View Solution