In the given figure, AB is thechord of a circle with centre O, AB is produced to C such that BC=OB, CO is joined and produced to meet the circle in D if ∠ACD=y∘and∠AOD=x∘, then prove that ∠OAB=(23)x∘.
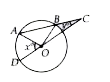
The correct Answer is:23x∘
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - NCERT Section (Exercise 10.1 (Fill in the blanks.))
10 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - NCERT Section (Exercise 10.2)
16 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Olympiad/HOTS Corner
30 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
AB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.
View SolutionAB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.
View Solution
Knowledge Check
AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
A48∘B96∘C108∘D80∘In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
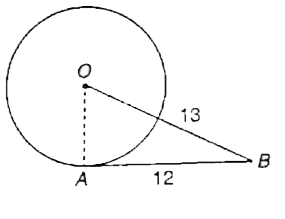 A6.5 cmB6 cmC5 cmDnone of these
A6.5 cmB6 cmC5 cmDnone of theseAB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘
In the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC = OB. The straight line Co is produced to meet the circle at D. If ACD = y and AOD = x, such that x = ky, then the value of k is.
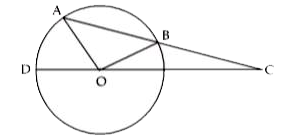
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the figure AB is the chord of a circle with centre O and DOC is a line segment such that BC=DO. If ∠C=20∘, find angle AOD.
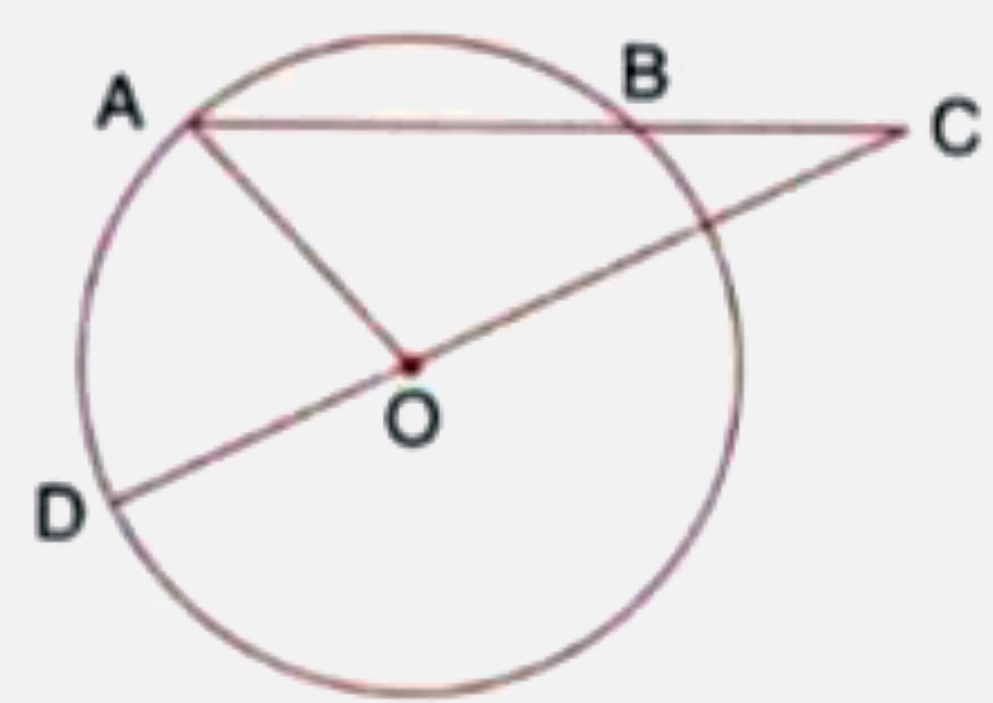
View SolutionIn Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
View SolutionIn the given figure,AB and BC are two chords of the circle with Centre O ,where ∠BAO=50∘,∠BCO=35∘,then ∠AOC is equal to
View Solution
