In the given fig., ABCD is a cyclic quadrilateral and PAT is a tangent line to the circle. If BD is a diameter of the circle, then which of the following is true ? 
All of these
The correct Answer is:D
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (LEVEL -2)
20 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Match the following)
6 Videos
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - NCERT Section (Exercise 10.2)
16 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
 A40∘B50∘C60∘D30∘
A40∘B50∘C60∘D30∘In the adjoining figure BD is the diameter of the circle and ∠BCA=41∘. Find ∠ABD:
 A41∘B49∘C22.5∘D20.5∘
A41∘B49∘C22.5∘D20.5∘ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC=130∘ . Then angle BAC is equal to:
A150∘B40∘C50∘D60∘
In the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
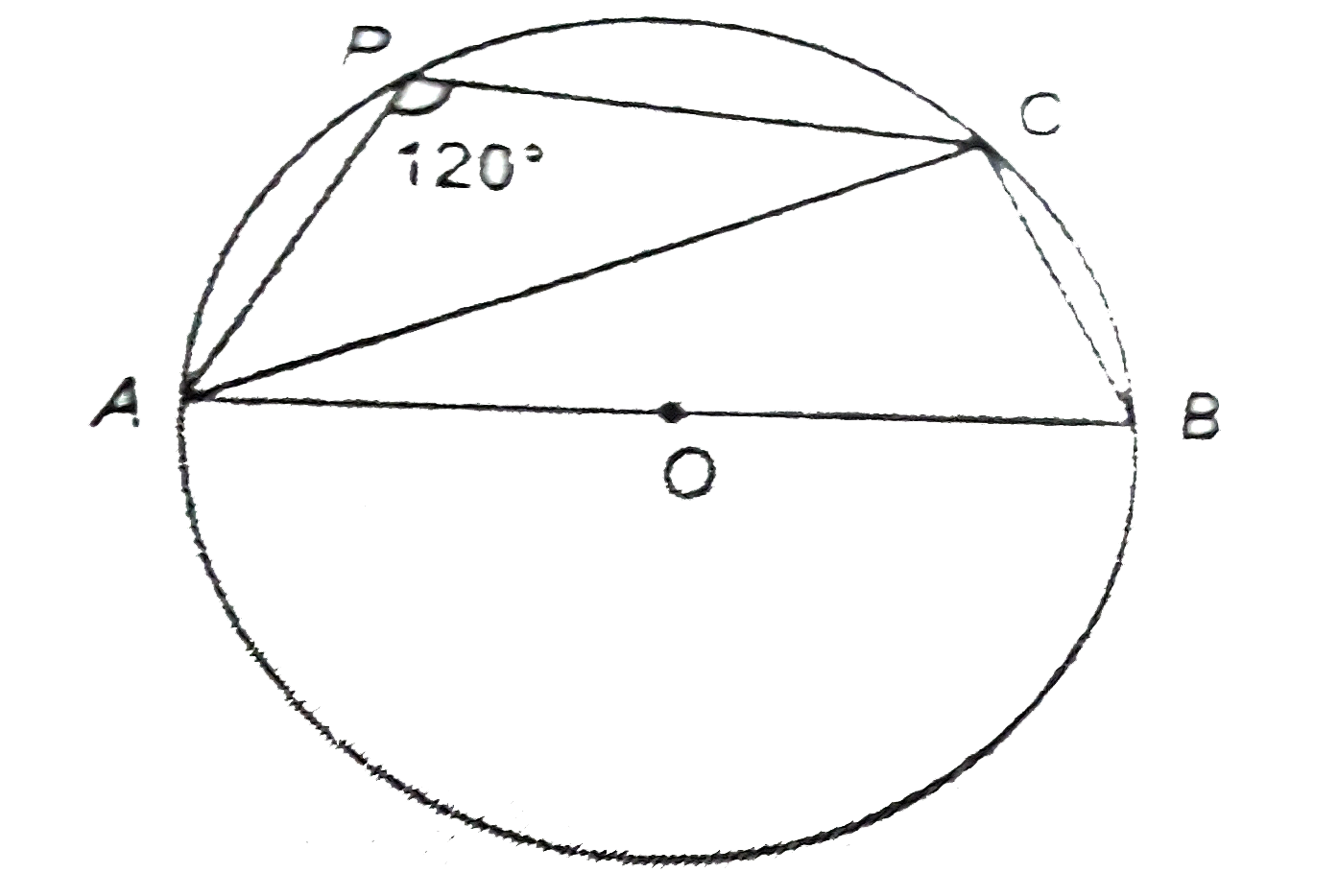
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.

View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View Solution
In the above figure, ABCD is a cyclic quadrilateral and ∠BCD=2∠BAD. Find the angle made by the diagonal BD at the centre of the circle.
View Solution
