The two cirles intersect at C and D, where O is the centre of the second circle. Produced AD cuts the second circle at F. Produced BD cuts the second circle at E. ∠DEF=110∘,∠ACB=32∘and∠DAB=118∘.
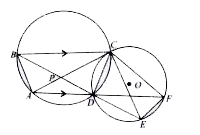
Find (i) ∠ACE(ii)∠COD
(i)−96∘,(ii)−68∘
(i)72∘,59∘
(i)59∘,(ii)72∘
(i)68∘,(ii)96∘
The correct Answer is:D
Topper's Solved these Questions
- CIRCLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLESEXERCISE - Exercise (Comprehension (Passage-III))
4 Videos
- ARITHMETIC PROGRESSIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- CO-ORDINATE GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Olympiad/HOTS Corner
40 Videos
Similar Questions
In Figure, two circles intersect at A and B . The centre of the smaller circle is O and it lies on the circumference of the larger circle. If ∠APB=700, find ∠ACB
View SolutionIn the figure PQ is a diameter of a circle with centre O. QR is a tangent to the circle equal to OQ. OT is perpendicular to PR. QT is produced to cut the circle at S Prove that SP=ST
View Solution
Knowledge Check
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmAB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
A20∘B30∘C40∘D60∘
In the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
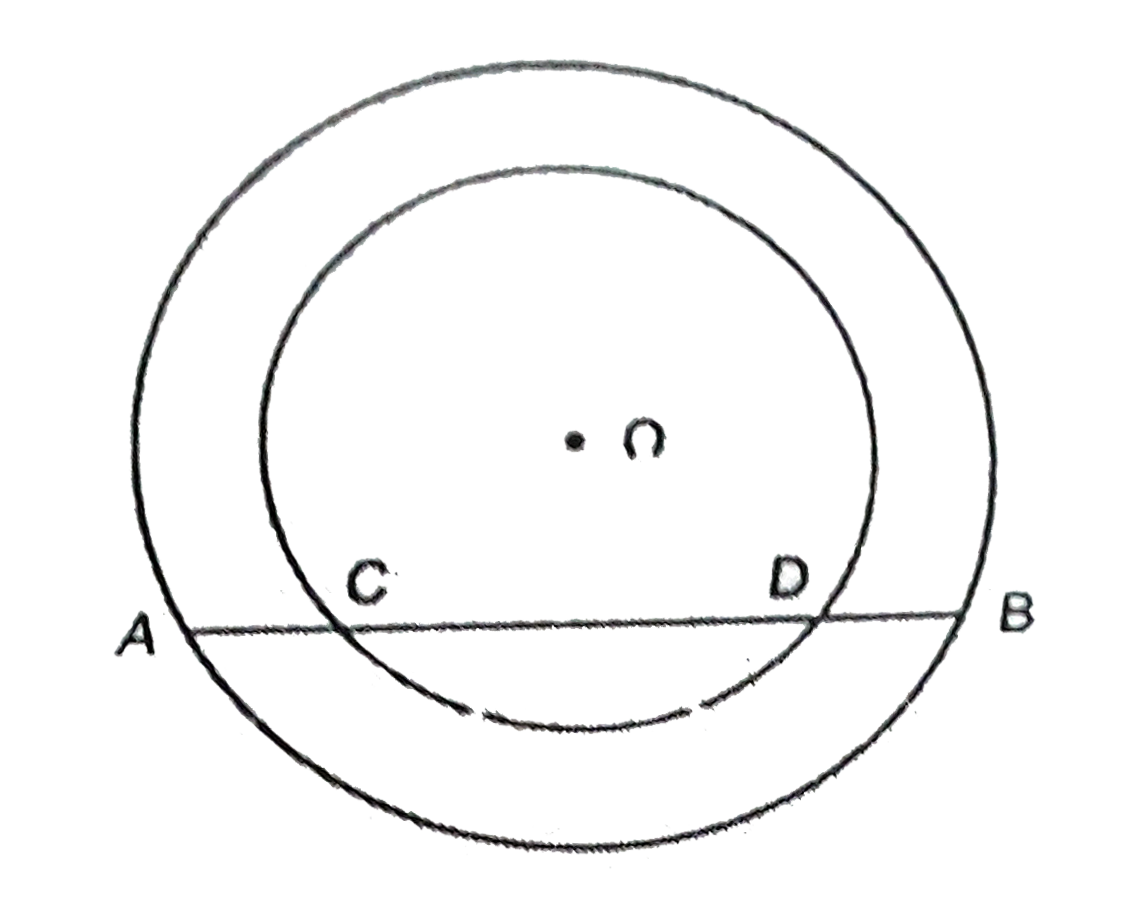
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.

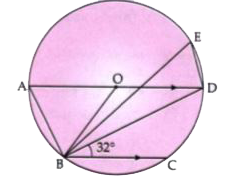
View SolutionIn the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD=32∘. Find : (i) ∠OBD (ii) ∠AOB (iii) ∠BED
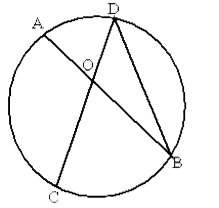
View SolutionAB is a diameter of the circle. Two points C and D are such point that CD = BD. AB and CD intersect at O. If angle ∠AOD=45∘. Find ∠ADC
View SolutionIn the given figure o is the centre of the two concentric circles. A line T cuts the circles at A, B, C and D as shown in the figure. OP is perpendicular to AD.
Given OA = 34 cm, OP = 16 cm and AB = 18 cm Find :
radius of the smaller circle
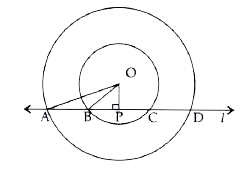
View SolutionIn the given figure o is the centre of the two concentric circles. A line T cuts the circles at A, B, C and D as shown in the figure. OP is perpendicular to AD.
Given OA = 34 cm, OP = 16 cm and AB = 18 cm Find :
length of chord AD

View Solution
