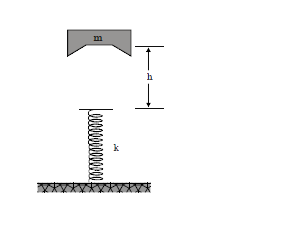
A block of mass 2kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. The maximum distance through which the spring will be compressed, is
0.11m
0.33m
0.22m
0.44m
The correct Answer is:B
Here m=2kg, h=1m, k= 490Nm−1. Let the spring be compressed through distance x. Then the block falls through a height (h+x). Gain in P.E of the spring = Loss in P.E. of the block
12kx2=mg(h+x)
or 12×490×x2=2×9.8×(1+x)
or 12.5x2−x−1=0
∴x=1±√1+4×12.52×12.5=1±√5125=0.33m
Topper's Solved these Questions
- WORK AND ENERGYBook:MTG IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:Exercise (Comprehension Type)
Explore 5 Videos
- WORK AND ENERGYBook:MTG IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:Exercise (Subjective Problems Very short Answer Type)
Explore 16 Videos
- WORK AND ENERGYBook:MTG IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:Exercise (Multiple Choice Questions Level -1)
Explore 30 Videos
- THRUST AND PRESSUREBook:MTG IIT JEE FOUNDATIONChapter:THRUST AND PRESSUREExercise:Olympiad/HOTS Corner
Explore 15 Videos
Similar Questions
A block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View Solution
Knowledge Check
A block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5cmB15cmC26cmD10cmA block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2
A block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA spring gets compressed when a body of mass 5 g is dropped on it from a height of 2 m . Calculate the maximum distance s through whichthe spring is compressed. The force constant of spring is 100Nm−1 .
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
