Question

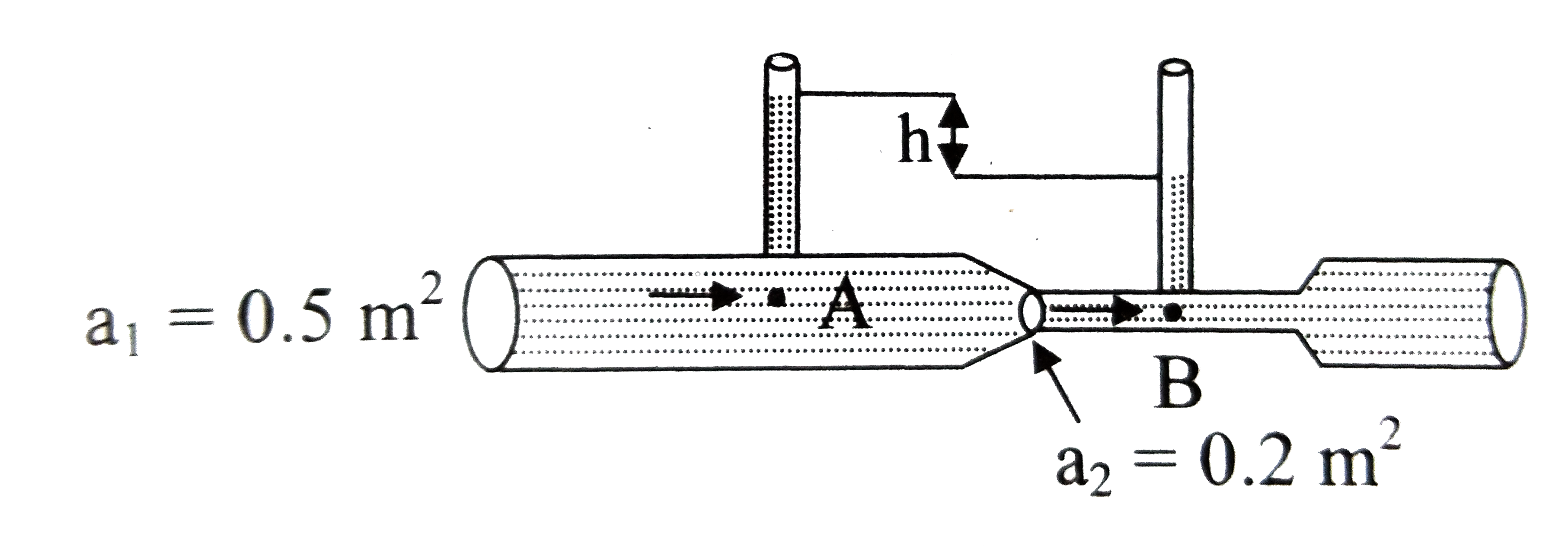
A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section ${\displaystyle A_1}$ and ${\displaystyle A_2}$ are ${\displaystyle v_1}$ and ${\displaystyle v_2}$ respectively. The difference in the levels of the liquid in the two vertical tubes is ${\displaystyle h}$. Then

Options

A. The volume of the liquid flowing through the tube in unit time is `A_1v_1`
B. `v_2-v_1=sqrt(2gh)`
C. `v_2^2-v_1^2 = 2gh`
D. The energy per unit mass of the liquid is the same in both sections of the tube

Answer

A::C::D

Explanation

According to equation of continuity -
`A_1 v_1=A_2 v_2" "(a) rarr` correct
According to Bernoulli.s theorem
`P_1+1/2 rho v_1^2=P_2+1/2 rho v_2^2`
`implies P_1-P_2 = 1/2 rho(v_2^2-v_1^2)=rho gh=1/2 rho(v_2^2-v_1^2)`
`implies 2gh=v_2^2-v_1^2" "(c) rarr` correct
According to Bernoulli.s theorem `(d) rarr` correct