The terminal velocity (vt) of the spherical raindrop depends on the radius (r) of the spherical raindrop as
r
r2
1r
1r2
To determine the relationship between the terminal velocity vt of a spherical raindrop and its radius r, we can analyze the forces acting on the raindrop as it falls through the air.
1. Understanding Forces Acting on the Raindrop:
- When a raindrop falls, it experiences three main forces:
- The gravitational force (weight) acting downwards, Fg=mg, where m is the mass of the raindrop and g is the acceleration due to gravity.
- The buoyant force acting upwards, which can be given by Archimedes' principle.
- The viscous drag force acting upwards, which opposes the motion of the raindrop.
2. Establishing the Condition for Terminal Velocity:
- Terminal velocity is reached when the net force acting on the raindrop is zero. This occurs when the downward gravitational force equals the sum of the upward buoyant force and the viscous drag force:
mg=Fb+Fd
- Here, Fb is the buoyant force and Fd is the viscous drag force.
3. Calculating the Forces:
- The buoyant force Fb can be expressed as:
Fb=ρLVg
where ρL is the density of the liquid (air in this case) and V is the volume of the raindrop, which for a sphere is given by V=43πr3.
- The viscous drag force Fd for a sphere moving through a viscous medium can be expressed using Stokes' law:
Fd=6πηrvt
where η is the coefficient of viscosity of the medium.
4. Setting Up the Equation:
- Substituting the expressions for Fb and Fd into the equilibrium condition:
mg=ρL(43πr3)g+6πηrvt
5. Solving for Terminal Velocity:
- Rearranging the equation to solve for vt:
mg−ρL(43πr3)g=6πηrvt
- This simplifies to:
vt=mg−ρL(43πr3)g6πηr
- Substituting m=ρsV=ρs(43πr3):
vt=ρs(43πr3)g−ρL(43πr3)g6πηr
- Factoring out common terms:
vt=g(ρs−ρL)(43πr3)6πηr
- Simplifying further:
vt=2g(ρs−ρL)r29η
6. Final Relationship:
- Thus, we find that the terminal velocity vt is directly proportional to the square of the radius r:
vt∝r2
Conclusion:
The correct relationship between the terminal velocity vt of a spherical raindrop and its radius r is:
vt∝r2
- When a raindrop falls, it experiences three main forces:
- The gravitational force (weight) acting downwards, Fg=mg, where m is the mass of the raindrop and g is the acceleration due to gravity.
- The buoyant force acting upwards, which can be given by Archimedes' principle.
- The viscous drag force acting upwards, which opposes the motion of the raindrop.
- Terminal velocity is reached when the net force acting on the raindrop is zero. This occurs when the downward gravitational force equals the sum of the upward buoyant force and the viscous drag force:
mg=Fb+Fd
- Here, Fb is the buoyant force and Fd is the viscous drag force.
- The buoyant force Fb can be expressed as:
Fb=ρLVg
where ρL is the density of the liquid (air in this case) and V is the volume of the raindrop, which for a sphere is given by V=43πr3.
- The viscous drag force Fd for a sphere moving through a viscous medium can be expressed using Stokes' law:
Fd=6πηrvt
where η is the coefficient of viscosity of the medium.
- Substituting the expressions for Fb and Fd into the equilibrium condition:
mg=ρL(43πr3)g+6πηrvt
- Rearranging the equation to solve for vt:
mg−ρL(43πr3)g=6πηrvt
- This simplifies to:
vt=mg−ρL(43πr3)g6πηr
- Substituting m=ρsV=ρs(43πr3):
vt=ρs(43πr3)g−ρL(43πr3)g6πηr
- Factoring out common terms:
vt=g(ρs−ρL)(43πr3)6πηr
- Simplifying further:
vt=2g(ρs−ρL)r29η
- Thus, we find that the terminal velocity vt is directly proportional to the square of the radius r:
vt∝r2
The correct relationship between the terminal velocity vt of a spherical raindrop and its radius r is:
vt∝r2
Topper's Solved these Questions
Similar Questions
Knowledge Check
Terminal velocity (V) of a spherical object varies with a radius of object (r) -
A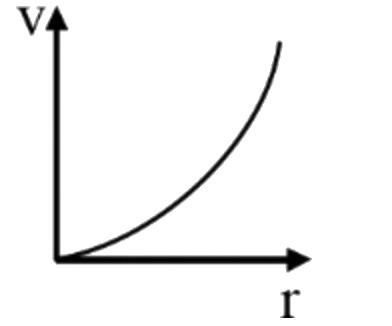 B
B C
C D
D
The terminal velocity V of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
AVR= ConstantBVR= constantCV= constantDVR2= constantThe terminal velocity of small sized spherical body of radius r falling vertically in a viscous liquid is given by the following proportionality
A1r2Br2C1rDr
Velocity OF image in Spherical mirror
View SolutionA small spherical ball falling through a viscous medium of negligible density has terminal velocity v. Another ball of the same mass but of radius twice that of the earlier falling through the same viscous medium will have terminal velocity
View SolutionA sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
View SolutionThe nature of graph between terminal velocity of spherical body vs the square of its radius is
View SolutionTwo rain drops of same radius r falling with terminal velocity v merge and from a bigger drop of radius R. The terminal velocity of the bigger drop is
View Solution
