A soap bubbles of radius 6cm and 9cm respectively placed in contact with each other. Find the radius of curvature of interface is.
18
16
12
10
To find the radius of curvature of the interface between two soap bubbles of radii 6 cm and 9 cm, we can follow these steps:
1. Identify the Radii of the Soap Bubbles:
- Let the radius of the first soap bubble, r1=6 cm.
- Let the radius of the second soap bubble, r2=9 cm.
2. Understand the Concept of Excess Pressure:
- The excess pressure inside a soap bubble is given by the formula:
P=4Tr
where T is the surface tension of the soap solution and r is the radius of the bubble.
3. Calculate the Excess Pressures:
- For the first bubble:
P1=4Tr1=4T6
- For the second bubble:
P2=4Tr2=4T9
4. Set Up the Equation for the Interface:
- When the two bubbles are in contact, the pressure difference between them is equal to the pressure inside the new bubble (let's denote its radius as R):
P1−P2=4TR
- Substituting the expressions for P1 and P2:
4T6−4T9=4TR
5. Simplify the Equation:
- Factor out 4T:
4T(16−19)=4TR
- Cancel 4T from both sides (assuming T≠0):
16−19=1R
6. Find a Common Denominator:
- The common denominator for 6 and 9 is 18:
318−218=1R
- This simplifies to:
118=1R
7. Solve for R:
- Taking the reciprocal gives:
R=18 cm
Final Answer:
The radius of curvature of the interface between the two soap bubbles is 18 cm.
- Let the radius of the first soap bubble, r1=6 cm.
- Let the radius of the second soap bubble, r2=9 cm.
- The excess pressure inside a soap bubble is given by the formula:
P=4Tr
where T is the surface tension of the soap solution and r is the radius of the bubble.
- For the first bubble:
P1=4Tr1=4T6
- For the second bubble:
P2=4Tr2=4T9
- When the two bubbles are in contact, the pressure difference between them is equal to the pressure inside the new bubble (let's denote its radius as R):
P1−P2=4TR
- Substituting the expressions for P1 and P2:
4T6−4T9=4TR
- Factor out 4T:
4T(16−19)=4TR
- Cancel 4T from both sides (assuming T≠0):
16−19=1R
- The common denominator for 6 and 9 is 18:
318−218=1R
- This simplifies to:
118=1R
- Taking the reciprocal gives:
R=18 cm
The radius of curvature of the interface between the two soap bubbles is 18 cm.
Topper's Solved these Questions
Similar Questions
Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionTwo soap bubbles of radii 4cm and 6 cm are in contact with each other. What is the radius of the common boundary?
View Solution
Knowledge Check
If two bubble of radii 0.03 cm and 0.04 cm come in contact with each other then the radius of curvature of the common surface 'r' is given by.
A0.03B0.06C0.12D0.24Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:
AinfiniteB2rCrDr/2Two soap bubbles one of radius 50 mm and the other of radius 80 mm are brought together so that they have a common interface.
(b) The radius of curvature of this interface attains which shape from smaller bubble towards larger bubble.AConvexBConcaveCPlaneDNone
Two soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
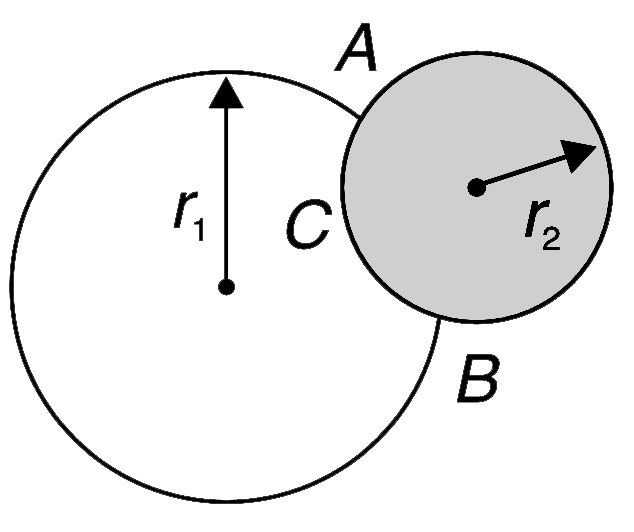
View SolutionA spherical soap bubble of radius 2 cm attached to the outside of a spherical bubble of radius 4 cm. Find the radius of curvature of the common surface.
View SolutionDraw a line segment AB of length 9cm. With A and B as centres, draw circles of radius 5cm and 3cm respectively. Construct tangents to each circle from the centre of the other circle.
View Solution
