Capacitor C and d changed to d/2. Find new C.
0.084027777777778
0.043055555555556
0.042361111111111
0.16736111111111
To solve the problem of finding the new capacitance C′ when the distance d between the plates of a capacitor is changed to d2, we can follow these steps:
Step 1: Understand the formula for capacitance
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where:
- ε0 is the permittivity of free space,
- A is the area of one of the plates,
- d is the distance between the plates.
Step 2: Write the initial capacitance
Given the initial distance between the plates is d, we can express the initial capacitance as:
C=ε0Ad
Step 3: Determine the new distance
The new distance between the plates is given as d2.
Step 4: Write the new capacitance formula
Using the new distance, the new capacitance C′ can be expressed as:
C′=ε0Ad2
Step 5: Simplify the new capacitance
We can simplify the expression for C′:
C′=ε0Ad2=ε0A⋅2d=2⋅ε0Ad=2C
Conclusion
Thus, the new capacitance C′ when the distance is changed to d2 is:
C′=2C
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where:
- ε0 is the permittivity of free space,
- A is the area of one of the plates,
- d is the distance between the plates.
Given the initial distance between the plates is d, we can express the initial capacitance as:
C=ε0Ad
The new distance between the plates is given as d2.
Using the new distance, the new capacitance C′ can be expressed as:
C′=ε0Ad2
We can simplify the expression for C′:
C′=ε0Ad2=ε0A⋅2d=2⋅ε0Ad=2C
Thus, the new capacitance C′ when the distance is changed to d2 is:
C′=2C
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor has plate A and separation d between the plates. The capacitor is connected to a battery of emf V. (a) find the charge on the capacitor. (b) the plate separation is decreases to d/2. Find the extra charge given by the battery to the positive plate. (c) work done in reducing separation between plates.
View SolutionSeparation between the plates of a capacitor is increased from d to 2d while the battery remains connected with the plates. How will the stored energy in the capacitor change?
View Solution
Knowledge Check
A capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
AVC1C1+C2BVC2C1+C2CVC1C2C1+C2DVC1+C2Two capacitors C1 and C2 are charged separately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectively. A is connected with CandB is connected with D.
i. Find the final potential difference across each capacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.A128μC 142μC 60uJB28μC 42μC 60uJC28μC 42μC 160uJD2.8μC 4.2μC 60uJConsider the circuit shown in the figure. Find the charge on capacitor C between A and D in steady state.
 ACεBCε/2CCε/3Dzero
ACεBCε/2CCε/3Dzero
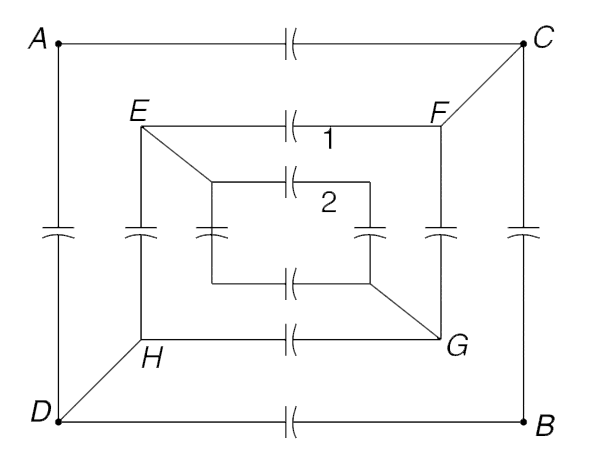
In the circuit shown in the figure all the capacitors have capacitance C.
(a) Find the charge on capacitors marked as 1 and 2 when a battery of emf V is connected across points A and B.
(b) Find the equivalent capacitance across points C and D marked in the Figure.
(c) Find the equivalent capacitance across points E and G.
View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionFor the network of capacirors as shown in.
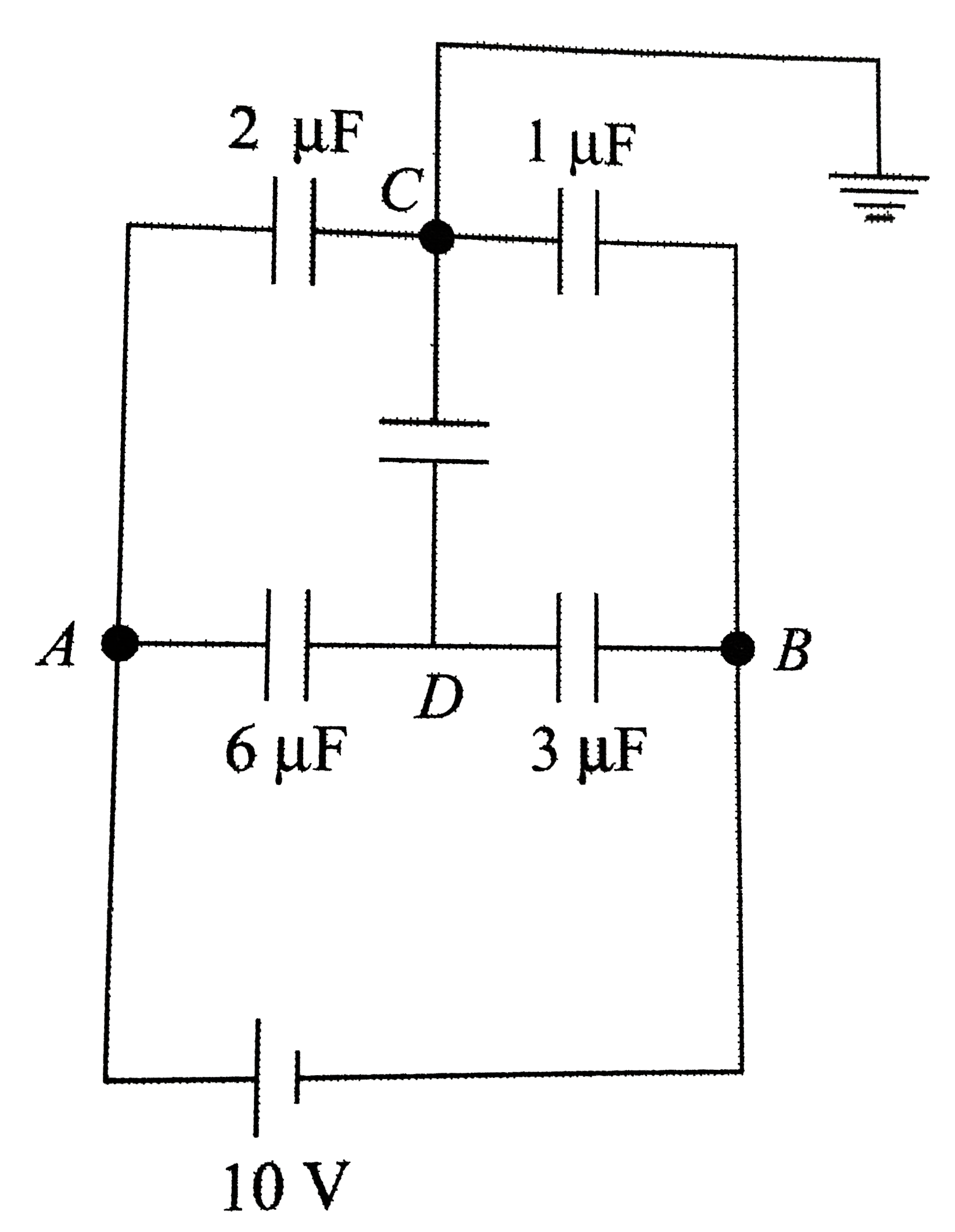 .
.
a. Find the potential of junction D.
b. Find the potential of function D,
c. Find the charge on 2μF capacitor.
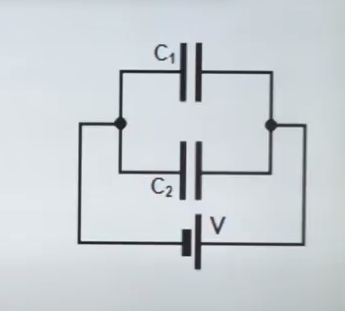
View SolutionTwo capacitor C1 with capacitance 2C and C2 with capacitance C are connected in parallel. They are changed and then the batter is removed. If a material of dielectric constant K is inserted in C2. Find final potential across them.
View SolutionA Capacitor blocks d.c. and allows a.c. Why ?
View Solution
