In the given diagram assuming a1, a2, a3, a4 upwards the correct relation is
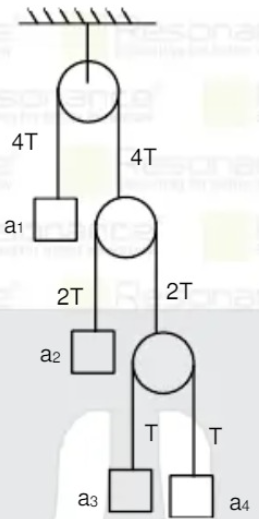
4a1−2a2−a3−a4=0
4a1+2a2+a3+a4=0
2a1+4a2+4a3+a4=0
4a1−2a2+a3+a4=0
Step by step video & image solution for In the given diagram assuming a_1, a_2, a_3, a_4 upwards the correct relation is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆkandˆl,and→a1,→a2,→a3,→a4 are four non-zero vectors such that no vector can be expressed as a linear combination of others and (λ−1)(→a1−→a2)+μ(→a2+→a3)+γ(→a3+→a4−2→a2)+→a3+δ→a4=0, then a. λ=1 b. μ=−2/3 c. γ=2/3 d. δ=1/3
View SolutionThe average of a1,a2,a3,a4 is 16. Half of the sum of a2,a3,a4 is 23. What is the value of a1
View Solution
Knowledge Check
The number of permutations of the letters a1,a2,a3,a4,a5 in which the first letter a1 does not occupy the first position (from the left) and the second letter a2 does not occupy the second position (from the left) is
A96B78C60D42The number of all three elements subsets of the set {a1,a2,a3….an} which contain a3 is
AnC3Bn−1C3Cn−1C2Dnone of theseThe probability that a man who is 85 years old will die before attaining the age of 90 is 1/3. Four persons A1,A2,A3 and A4 are 85 years old. The probability that A1 will die before attaining the age of 90 and will be the first to die is
A6581B1381C65324D13108
Three rectangles A1, A2 and A3 have the same area. Their lengths a1, a2 and a3 respectively are such that a1<a2<a3 . Cylinders C1, C2 and C3 are formed from A1, A2 and A3 respectively by joining the parallel sides along the breadth. Then C1 will enclosed maximum volume (b) C2 will enclosed maximum volume (c) C3 will enclosed maximum volume (d) Each of C1, C2 and C3 will enclose equal volume
View SolutionConsider the following statements : A number a1a2a3a4a5 is divisible by 9 if
1. a1+a2+a3+a4+a5 is divisible by 9.
2. a1−a2+a3−a4+a5 is divisible by 9.
Which of the above statements is/are correct?
View SolutionThe number of ordered quadruples (a1,a2,a3,a4) of positive odd integers that satisfy a1+a2+a3+a4=32 is equal to (a)31C3 (b) 17C3 (c)4495 (d) (17C3)−(17C4)
View SolutionLet 6 Arithmetic means A1,A2,A3,A4,A5,A6 are inserted between two consecutive natural number aandb(a>b). If A21−A22+A23−A24+A25−A26 is equal to prime number then 'b' is equal to
View SolutionIn an arithmetic sequence a1+a3=12 and a4+a6=24. Find the values of a and d
View Solution
