A man standing on ground observes that rain is coming at an agle with vertical. When he runs with speed km/hr rain appears to him vertical. Find speed of rain w.r.t man.
km/hr
km/hr
km/hr
km/hr
To solve the problem, we need to analyze the situation using the concept of relative velocity. Let's break it down step by step:
Step 1: Understand the Situation
The man observes the rain coming at an angle of 45∘ with the vertical when he is standing still. This implies that the horizontal and vertical components of the rain's velocity are equal.
Step 2: Set Up the Velocity Components
Let the speed of the rain with respect to the ground be vr. Since the rain makes a 45∘ angle with the vertical, we can express the components of the rain's velocity:
- Vertical component: vry=vrcos(45∘)=vr√2
- Horizontal component: vrx=vrsin(45∘)=vr√2
Step 3: Analyze the Man's Motion
When the man runs with a speed of 15√2 km/hr, the rain appears to him to be falling vertically. This means that the horizontal component of the rain's velocity must be equal to the man's running speed to cancel each other out.
Step 4: Set Up the Equation
Since the rain appears vertical to the man, we can set the horizontal component of the rain's velocity equal to the man's speed:
vrx=15√2 km/hr
Substituting vrx:
vr√2=15√2
Step 5: Solve for the Rain's Speed
Now, we can solve for vr:
vr=15√2⋅√2=15⋅2=30 km/hr
Conclusion
Thus, the speed of the rain with respect to the man is 30 km/hr.
---
The man observes the rain coming at an angle of 45∘ with the vertical when he is standing still. This implies that the horizontal and vertical components of the rain's velocity are equal.
Let the speed of the rain with respect to the ground be vr. Since the rain makes a 45∘ angle with the vertical, we can express the components of the rain's velocity:
- Vertical component: vry=vrcos(45∘)=vr√2
- Horizontal component: vrx=vrsin(45∘)=vr√2
When the man runs with a speed of 15√2 km/hr, the rain appears to him to be falling vertically. This means that the horizontal component of the rain's velocity must be equal to the man's running speed to cancel each other out.
Since the rain appears vertical to the man, we can set the horizontal component of the rain's velocity equal to the man's speed:
vrx=15√2 km/hr
Substituting vrx:
vr√2=15√2
Now, we can solve for vr:
vr=15√2⋅√2=15⋅2=30 km/hr
Thus, the speed of the rain with respect to the man is 30 km/hr.
Topper's Solved these Questions
Similar Questions
When a boy is stationary, he observes that rain drops are falling at 30∘ to vertical direction. When he starts running with speed 10ms, he observed that rain drops are falling vertically downwards. Calculate the actual velocity of rain drops.
View SolutionA man is coming down an incline of angle 30∘ . When he walks with speed 2√3m/s he has to keep his umbrella vertical to protect hismself from rain. The actual speed of rain is 5m/s . At what angle with vertical should he keep his umbrella when he is at rest so that he does not get drenched ?
View Solution
Knowledge Check
A man is standing on a road and observes that rain is failing at angle 45∘ with the vertical. The man starts running on the road with constant acceleration 0.5m/s2. After a certain time from the start of the motion, it appears to him that rain is still falling at angle 45∘ with the vertical, with speed 2√2m/s. Motion of the man is in the same vertical plane in which the rain is falling. Then which of the following staement(s) are true.
Ait is not possibleBSpeed of the rain relative to the ground is 2m/sCSpeed of the man when he finds rain to be falling at angle 45∘ with the vertical, is 4m/s.DThe man has travelled a distance 16cm on the road by the time he again finds rain to be falling at angle 45∘Rain is falling with a sped of 12√2m/s at an angle 45∘ with the vertical line. A man in a glider going at a speed of u at an angle of 37∘ with respect to the ground. Find the speed of the glider so that rain appears to him falling vertically. Consider the motion of the glider and rain drops in the same vertical plane.
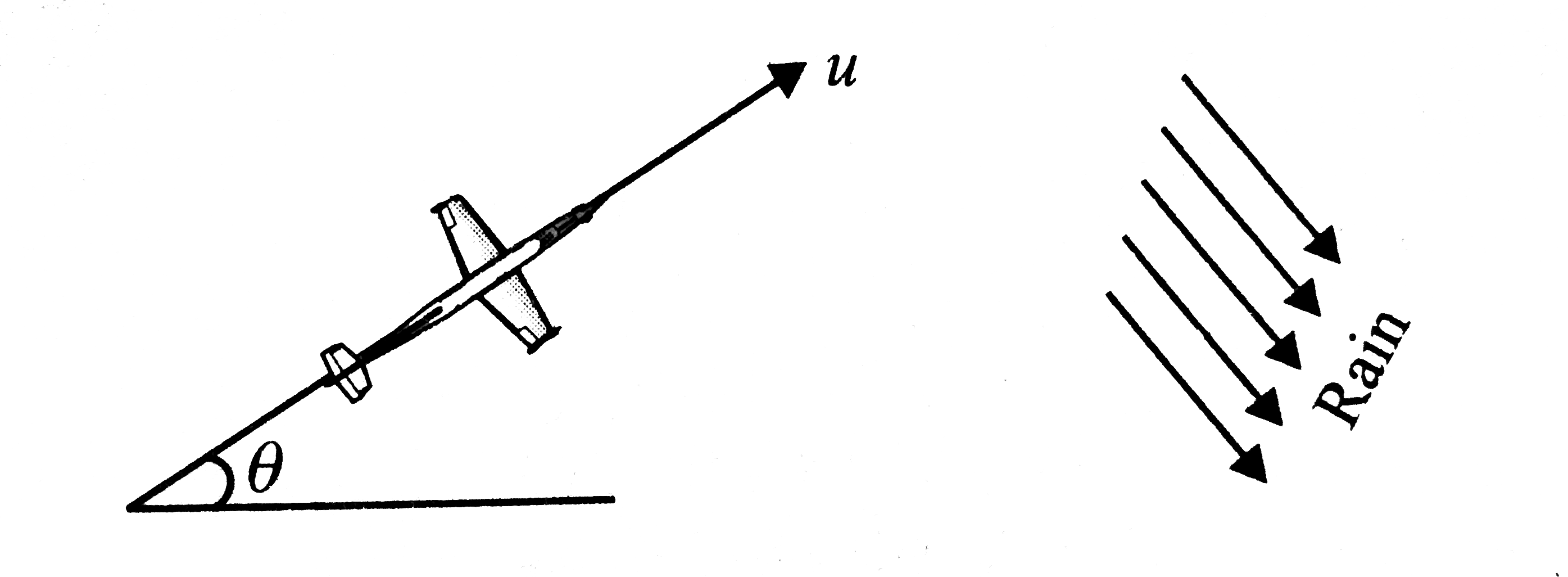 A15ms−1B30ms−1C10ms−1D25ms−1
A15ms−1B30ms−1C10ms−1D25ms−1To a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertical. Find the speed of rain.
A√2km/hB2√2km/hC3√2km/hD5√2km/h
A man is coming down an incline of angle 30∘. When he walks with speed 2(√3)ms−1 he has to keep his umbrella vertical to protect himself from rain. The actual speed of rain is 5ms−1. At angle with vertical should he keep his umbrella when he is at rest so that he does not getb drenched ?
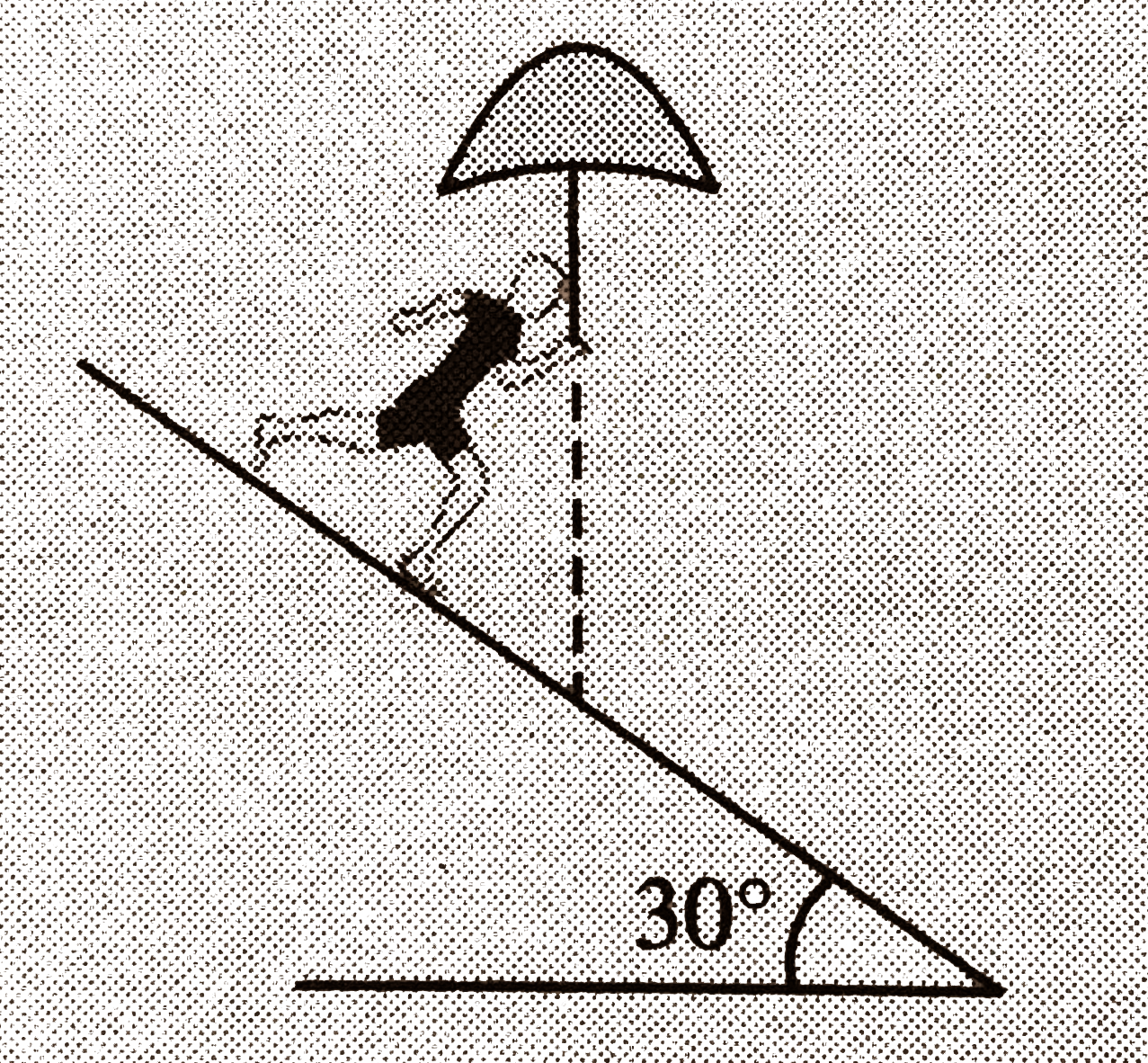 .
.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionIf a man is running on horizontal road, raise appears to him coming at 30∘ from vertical. When he double his velocity rain appears to him coming at angle θ from vertical. Then θ is
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View Solution
