Statement 1- An electron jumps from lower energy state E1 to higher energy state E2 then the photon energy absorbed is given as hv=E1−E2
Statement 2- An electron jumps from higher energy state E2 to lower energy state E1 then the photon energy released is given by hv=E2−E1
both are true
S1 is true S2 is false
S1 is false S2 is true
both are false
To solve the problem, we need to analyze the two statements given about the energy transitions of an electron in an atom.
1. Understanding Energy States:
- An electron can occupy different energy states in an atom. Let's denote the lower energy state as E1 and the higher energy state as E2.
- The energy difference between these states is ΔE=E2−E1.
2. Analyzing Statement 1:
- Statement 1 claims: "An electron jumps from lower energy state E1 to higher energy state E2, then the photon energy absorbed is given as hν=E1−E2".
- This statement is incorrect. When an electron absorbs energy to jump from a lower energy state to a higher energy state, the energy absorbed is equal to the difference in energy between the two states, which is hν=E2−E1.
- Therefore, Statement 1 is false.
3. Analyzing Statement 2:
- Statement 2 claims: "An electron jumps from higher energy state E2 to lower energy state E1, then the photon energy released is given by hν=E2−E1".
- This statement is correct. When an electron transitions from a higher energy state to a lower energy state, it releases energy in the form of a photon, and the energy of the photon released is indeed equal to the difference in energy between the two states, which is hν=E2−E1.
- Therefore, Statement 2 is true.
4. Conclusion:
- Based on the analysis, we conclude that Statement 1 is false, and Statement 2 is true.
Final Answer:
- Statement 1 is false.
- Statement 2 is true.
- An electron can occupy different energy states in an atom. Let's denote the lower energy state as E1 and the higher energy state as E2.
- The energy difference between these states is ΔE=E2−E1.
- Statement 1 claims: "An electron jumps from lower energy state E1 to higher energy state E2, then the photon energy absorbed is given as hν=E1−E2".
- This statement is incorrect. When an electron absorbs energy to jump from a lower energy state to a higher energy state, the energy absorbed is equal to the difference in energy between the two states, which is hν=E2−E1.
- Therefore, Statement 1 is false.
- Statement 2 claims: "An electron jumps from higher energy state E2 to lower energy state E1, then the photon energy released is given by hν=E2−E1".
- This statement is correct. When an electron transitions from a higher energy state to a lower energy state, it releases energy in the form of a photon, and the energy of the photon released is indeed equal to the difference in energy between the two states, which is hν=E2−E1.
- Therefore, Statement 2 is true.
- Based on the analysis, we conclude that Statement 1 is false, and Statement 2 is true.
- Statement 1 is false.
- Statement 2 is true.
Topper's Solved these Questions
Similar Questions
Energy of an electron in the nth orbit of hydrogen atom is given by E,- ev. How much energy is required to take an electron from the ground state to the first excited state?
View SolutionThe energy of an electron in the nth orbit is given by En=−13.6/n2eV. Calculate the energy required to excite an electron from ground state to the second excited state.
View Solution
Knowledge Check
Amount of energy required to excite an electron of an atom from the lower energy state to its next higher energy state is defined as:
Aionization potentialBelectron afinityCcritical potentialDreduction potentialWhen an electron jumps from higher energy orbit to lower energy orbit, the difference in the energies in the two orbits is radiated as quantum (photon) of….
AE=mc2BE=hvℎCE=hcλDE=λhcThe ionisation energy of hydrogen is 13.6 eV . The energy of the photon released when an electron jumps from the first excited state (n=2) to the ground state of hydrogen atom is
A3.4 eVB4.53 eVC10.2 eVD13.6eV
Read the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
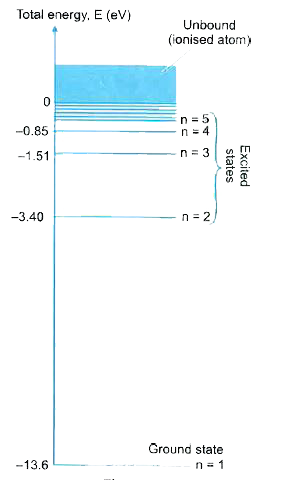
Now answer the follwoing questions:
How can a hydrogen atom receive energy to raise the electron to higher energy states ?
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
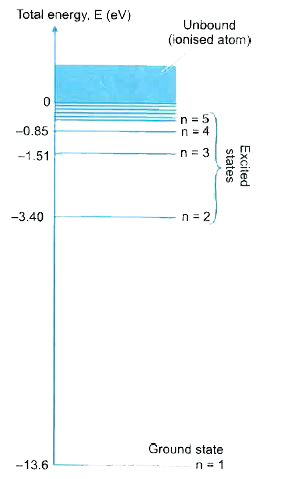
Now answer the follwoing questions:
When does a hydrogen atom emit a photon ?
View SolutionWhen electric transition occurs from higher energy state to lower energy state with energy difference equal to ΔE electron volts , the wavelkength of the line emitted is apporomately equal to
View SolutionThe total energy of an electron in the excited state corresponding to n =3 state is E. What is its potential energy with proper sign?
View SolutionGround state energy of H-atom is (−E1),t he velocity of photoelectrons emitted when photon of energy E2 strikes stationary Li2+ ion in ground state will be:
View Solution
