Three charged particles having charge q each are suspended by means of thread from a common point. In equilibrium triangle of side l. The electrostatic force on one of the charges is
2√3q24πε0l2
2q24πε0l2
q28πε0l2
√3q24πε0l2
To solve the problem of finding the electrostatic force on one of the charges in an equilateral triangle configuration with three charges q, we can follow these steps:
1. Understanding the Configuration:
We have three charges q each, placed at the vertices of an equilateral triangle with side length l. The charges repel each other due to their like charges.
2. Calculating the Electrostatic Force:
The electrostatic force F between any two charges q separated by a distance l is given by Coulomb's law:
F=k⋅q2l2
where k is Coulomb's constant.
3. Identifying Forces Acting on One Charge:
Let's consider one of the charges, say q1. It experiences repulsive forces due to the other two charges q2 and q3. The magnitude of the force exerted on q1 by q2 is F and similarly, the force exerted by q3 is also F.
4. Direction of Forces:
The forces F from q2 and q3 act along the lines connecting q1 to q2 and q1 to q3, respectively. The angle between these two forces is 60∘ because it is an equilateral triangle.
5. Calculating the Resultant Force:
To find the resultant force FR acting on q1, we can use the formula for the resultant of two vectors:
FR=√F2+F2+2F⋅F⋅cos(60∘)
Since cos(60∘)=12, we can simplify this to:
FR=√F2+F2+2F2⋅12=√F2+F2+F2=√3F2=F√3
6. Substituting the Value of F:
Now substituting F=k⋅q2l2:
FR=F√3=√3⋅k⋅q2l2
7. Final Expression:
If we express k in terms of ϵ0 (where k=14πϵ0), we get:
FR=√3⋅14πϵ0⋅q2l2=√3⋅q24πϵ0l2
Conclusion:
The electrostatic force on one of the charges is given by:
FR=√3⋅q24πϵ0l2
We have three charges q each, placed at the vertices of an equilateral triangle with side length l. The charges repel each other due to their like charges.
The electrostatic force F between any two charges q separated by a distance l is given by Coulomb's law:
F=k⋅q2l2
where k is Coulomb's constant.
Let's consider one of the charges, say q1. It experiences repulsive forces due to the other two charges q2 and q3. The magnitude of the force exerted on q1 by q2 is F and similarly, the force exerted by q3 is also F.
The forces F from q2 and q3 act along the lines connecting q1 to q2 and q1 to q3, respectively. The angle between these two forces is 60∘ because it is an equilateral triangle.
To find the resultant force FR acting on q1, we can use the formula for the resultant of two vectors:
FR=√F2+F2+2F⋅F⋅cos(60∘)
Since cos(60∘)=12, we can simplify this to:
FR=√F2+F2+2F2⋅12=√F2+F2+F2=√3F2=F√3
Now substituting F=k⋅q2l2:
FR=F√3=√3⋅k⋅q2l2
If we express k in terms of ϵ0 (where k=14πϵ0), we get:
FR=√3⋅14πϵ0⋅q2l2=√3⋅q24πϵ0l2
The electrostatic force on one of the charges is given by:
FR=√3⋅q24πϵ0l2
Topper's Solved these Questions
Similar Questions
Three particles have charges +10μ C each and they are fixed at the corners of an equilateral triangle of side 0.5m .The force on each of the particles has magnitude:
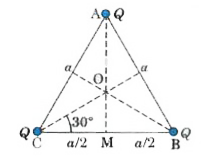
View SolutionThree identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
View Solution
Knowledge Check
Three charged particles are collinear and are in equilibrium, then
Aall the charged particles have the same polartiyBthe equilibrium is unstableCall the charged particles cannot have the same polarityDBoth (b) and (c ) are correctThree charged particle sare in equilibrium under their electrostatic forces only. Then
Athe particle smust be collinearBall the charges cannot have the same magnitudeCall the charges cannot have the same signDthe equilibrium is unstableTwo charged particles each having a charge +q and mass m are kept at a distance d. if they are in equilibrium under the gravitational force and the electric force between them, then the ratio qm or specific charge of each particle is
A√4πε0GB√4πε0GC4πε0GDG4πε0
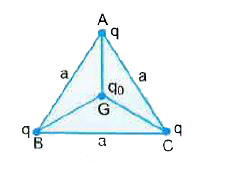
Three identical charges of q each are placed at the three verticess of an equilateral triangle ABC of side a, Electrostatic force experienced by a point charge q0 situated at the centroid G of triangle is ___________
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View SolutionCharge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
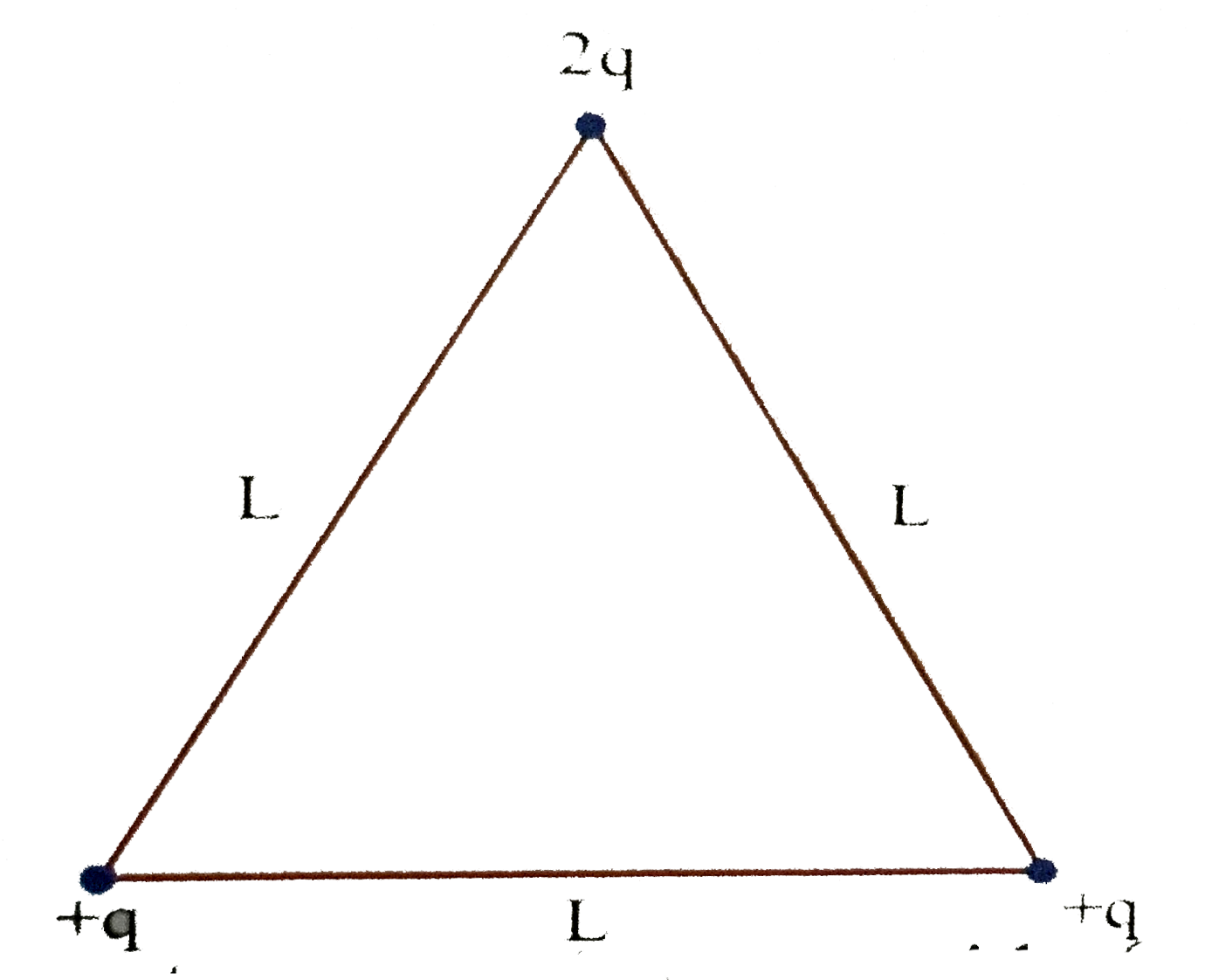
View Solutionthree points charges are placed at the cornors of an equilibrium triangle of side L as shown in the figure
View Solution
