A parallel beam strikes a sphere of RI 1.5 and diameter 30cm, the distance of image from centre of sphere will be 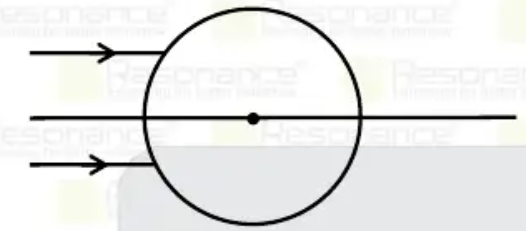
Step by step video & image solution for A parallel beam strikes a sphere of RI 1.5 and diameter 30cm, the distance of image from centre of sphere will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The diameter of a hollow metallic sphere is 60 cm and the sphere carries a charge of 500μC. The potential at a distance of 100cm from the centre of the sphere will be
A6×107VB7×106VC4.5×106VD5×106VA mark is made on the surface of a glass sphere of diameter 10 cm and refractive index 1.5. It is viewed through the glass from a portion directly opposite. The distance of the image of the mark from the centre of the sphere will be
A15 cmB17.5 cmC20 cmD22.5 cmA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
A−3RB+3RC−RD+R
A glass sphere of index 1.5 and radius 40 cm has half its hemispherical surface silvered.
The point where a parallel beam of light, coming along a diameter, will focus (or appear to) after coming out of sphere, will be :
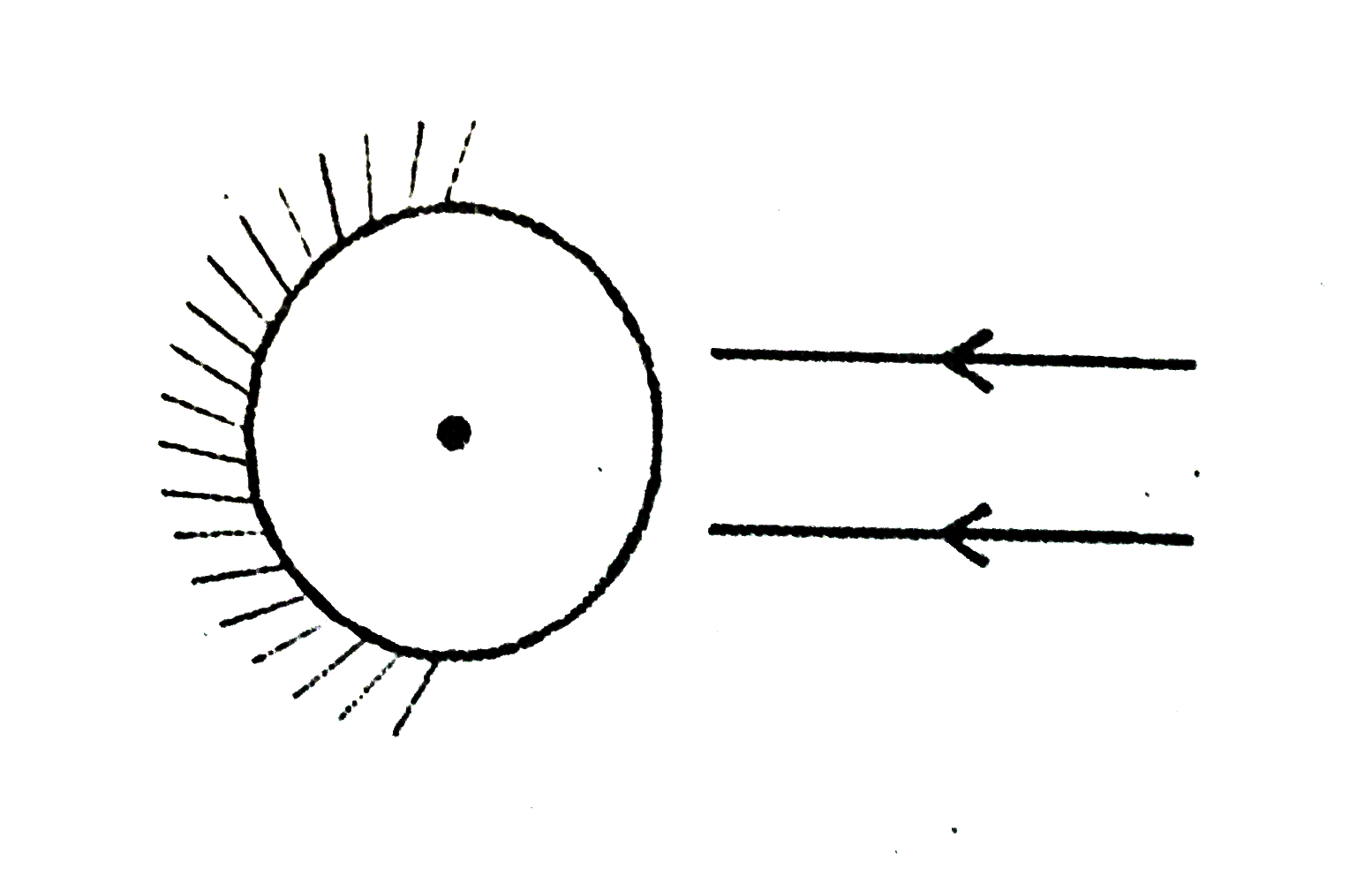
View SolutionA hollow sphere made of a transparent material of refractive index 1.5 has a small mark on its surface as shown. The mark is observed from the farther side. Find the distance of the image of mark from the centre of the sphere.

View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View SolutionThere is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
View SolutionA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View Solution
